题目内容
已知:二次函数y=x2+bx+c的图象与x轴交于A,B两点,其中A点坐标为(-3,0),与y轴 交于点C,点D(-2,-3)在抛物线上.
交于点C,点D(-2,-3)在抛物线上.
(1)求抛物线的解析式;
(2)抛物线的对称轴上有一动点P,求出PA+PD的最小值;
(3)点G抛物线上的动点,在x轴上是否存在点E,使B、D、E、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的E点坐标;如果不存在,请说明理由.
 交于点C,点D(-2,-3)在抛物线上.
交于点C,点D(-2,-3)在抛物线上.(1)求抛物线的解析式;
(2)抛物线的对称轴上有一动点P,求出PA+PD的最小值;
(3)点G抛物线上的动点,在x轴上是否存在点E,使B、D、E、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的E点坐标;如果不存在,请说明理由.
(1)将A(-3,0),D(-2,-3)代入y=x2+bx+c,得:
,
解得:
;
∴抛物线的解析式为:y=x2+2x-3.
(2)由:y=x2+2x-3得:
对称轴为:x=-
=-1,
令y=0,则:x2+2x-3=0,
∴x1=-3,x2=1,
∴点B坐标为(1,0),
而点A与点B关于x=-1对称,
∴连接BD与对称轴的交点即为所求的P点.
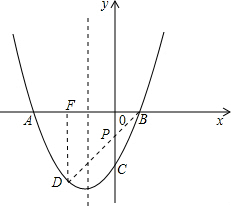 过点D作DF⊥x轴于点F,则:DF=3,BF=1-(-2)=3,
过点D作DF⊥x轴于点F,则:DF=3,BF=1-(-2)=3,
在Rt△BDF中,BD=
=3
,
∵PA=PB,
∴PA+PD=PB+PD=BD=3
,
即PA+PD的最小值为3
.
(3)存在符合条件的点E,
①在y=x2+2x-3中,令x=0,则有:y=-3,故点C坐标为(0,-3),
∴CD∥x轴,
∴在x轴上截取BE1=BE2=CD=2,得BCDE1和BDCE2,
此时:点C与点G重合,E1(-1,0),E2(3,0).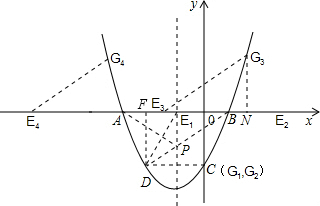
②∵BF=DF=3,∠DFB=90°,
∴∠FBD=45°,
当G3E3∥BD且相等时,有G3E3DB,作G3N⊥x轴于点N,
∵∠G3E3B=∠FBD=45°,∠G3NE3=90°,G3E3=BD=3
,
∴G3N=E3N=3;
将y=3代入y=x2+2x-3
得:x=-1±
,
∴E3的坐标为:(-1+
-3,0),
即(-4+
,0),
同理可得:E4(-4-
,0),
综上所述:存在这样的点E,所有满足条件的E点坐标为:
E1(-1,0),E2(3,0),
E3(-4+
,0),E4(-4-
,0).
|
解得:
|
∴抛物线的解析式为:y=x2+2x-3.
(2)由:y=x2+2x-3得:
对称轴为:x=-
| 2 |
| 2×1 |
令y=0,则:x2+2x-3=0,
∴x1=-3,x2=1,
∴点B坐标为(1,0),
而点A与点B关于x=-1对称,
∴连接BD与对称轴的交点即为所求的P点.
 过点D作DF⊥x轴于点F,则:DF=3,BF=1-(-2)=3,
过点D作DF⊥x轴于点F,则:DF=3,BF=1-(-2)=3,在Rt△BDF中,BD=
| 32+32 |
| 2 |
∵PA=PB,
∴PA+PD=PB+PD=BD=3
| 2 |
即PA+PD的最小值为3
| 2 |
(3)存在符合条件的点E,
①在y=x2+2x-3中,令x=0,则有:y=-3,故点C坐标为(0,-3),
∴CD∥x轴,
∴在x轴上截取BE1=BE2=CD=2,得BCDE1和BDCE2,
此时:点C与点G重合,E1(-1,0),E2(3,0).

②∵BF=DF=3,∠DFB=90°,
∴∠FBD=45°,
当G3E3∥BD且相等时,有G3E3DB,作G3N⊥x轴于点N,
∵∠G3E3B=∠FBD=45°,∠G3NE3=90°,G3E3=BD=3
| 2 |
∴G3N=E3N=3;
将y=3代入y=x2+2x-3
得:x=-1±
| 7 |
∴E3的坐标为:(-1+
| 7 |
即(-4+
| 7 |
同理可得:E4(-4-
| 7 |
综上所述:存在这样的点E,所有满足条件的E点坐标为:
E1(-1,0),E2(3,0),
E3(-4+
| 7 |
| 7 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


 不存在,请说明理由.
不存在,请说明理由.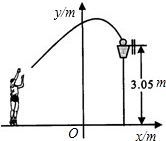 单位:m).请你根据所得的解析式,回答下列问题:
单位:m).请你根据所得的解析式,回答下列问题: C=OB,抛物线y=(x-2)(x-m)-(p-2)(p-m)(m、p为常数且m+2≥2p>0)经过A、C两点.
C=OB,抛物线y=(x-2)(x-m)-(p-2)(p-m)(m、p为常数且m+2≥2p>0)经过A、C两点.