题目内容
某商店将进价为40元的商品按50元售出时,每月可以售出500套.已知每涨0.5元销量就减少5个,若为赚8000元利润且销量又不超过300个,则售价应定为多少元?进货多少个?
考点:一元二次方程的应用
专题:销售问题
分析:设销售价x元/个,由于进货单价为40元的商品按50元出售时,能卖500个,已知该商品每涨价1元,其销量就要减少10个,所以现在能够卖[500-10(x-50)]个,每个利润为(x-40),而总利润为8000元,由此即可列出方程解决问题.
解答:解:设销售价x元/件.依题意得
[500-10(x-50)]•(x-40)=8000,
∴x2-140x+4800=0,
∴x=60或x=80,
当x=60时,500-10(x-50)=400,
当x=80时,500-10(x-50)=200,
∵进货量不能低于300件,
∴售价应定为60元/件,应进货400件.
答:售价应定为60元,此时应进货400件.
[500-10(x-50)]•(x-40)=8000,
∴x2-140x+4800=0,
∴x=60或x=80,
当x=60时,500-10(x-50)=400,
当x=80时,500-10(x-50)=200,
∵进货量不能低于300件,
∴售价应定为60元/件,应进货400件.
答:售价应定为60元,此时应进货400件.
点评:此题主要考查了一元二次方程的应用问题,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.

练习册系列答案
相关题目
 如图,将一个三角形绕其一边旋转一周后得到一个几何体,几何体的主视图和左视图都是边长为1的等边三角形,俯视图是一个圆,那么这个三角形的三条边长分别是多少?
如图,将一个三角形绕其一边旋转一周后得到一个几何体,几何体的主视图和左视图都是边长为1的等边三角形,俯视图是一个圆,那么这个三角形的三条边长分别是多少?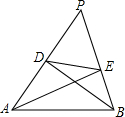 已知:在△PAB中,AE⊥BP,BD⊥AP,求证:△PDE∽△PBA.
已知:在△PAB中,AE⊥BP,BD⊥AP,求证:△PDE∽△PBA. 如图,已知数轴上有A、B两个点,它们表示的数分别是-24、-10.现有动点P从A点出发,以每秒3个单位长度的速度向右移动,与此同时,动点Q从B点出发,以每秒2个单位长度的速度向右移动,移动时间为t秒.
如图,已知数轴上有A、B两个点,它们表示的数分别是-24、-10.现有动点P从A点出发,以每秒3个单位长度的速度向右移动,与此同时,动点Q从B点出发,以每秒2个单位长度的速度向右移动,移动时间为t秒. 如图,D、E、F为△ABC的三边中点,L、M、N分别是△DEF三边的中点,若△ABC的周长为20cm,则△LMN的周长是
如图,D、E、F为△ABC的三边中点,L、M、N分别是△DEF三边的中点,若△ABC的周长为20cm,则△LMN的周长是