Question

【题目】如图，△ABC中，AB＝AC，∠BAC＝100°，将△ABC绕点A顺时针方向旋转40°得到△ADE，BC与AD、DE交于点G、F．

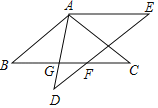
（1）求∠AGC的度数；

（2）求证：四边形ABFE是菱形．

Answer 1

【答案】（1）80°；（2）详见解析.

【解析】

（1）利用等腰三角形性质得出∠B＝∠C＝40°，利用旋转的性质和三角形的外角定理即可解答；

（2）利用平行线的判定定理证得AB∥DE，AE∥BF，所以四边形ABFE是平行四边形，再利用菱形判定定理即可解决问题.

解：（1）∵AB＝AC，∠BAC＝100°

∴∠B＝∠C＝40°，

∵将△ABC绕点A顺时针方向旋转40°得到△ADE，

∴AB＝AD，∠BAD＝40°，∠B＝∠D＝40°，∠BAC＝∠DAE＝120°，

∴∠AGC＝∠B+∠BAD＝80°

（2）∵∠D＝∠BAD＝40°，

∴AB∥DE，

∵∠DAE+∠AGC＝180°

∴AE∥BF

∴四边形ABFE是平行四边形，且AB＝AE，

∴四边形ABFE是菱形．