题目内容
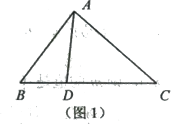
【题目】(1)如图1,△ABC中，D是BC边上一点，则△BD与△ADC有一个相同的高，它们的面积之比等于相应的底之比，记为
=
(△ABD、△ADC的面积分别用S△ABD、S△ADC表示)。现有BD=
BC,则S△ABD：S△ADC=
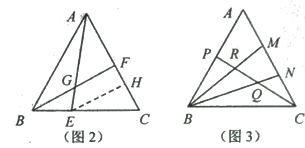
(2)如图2，△ABC中，E、F分别是BC、AC边上一点，且有BE:EC=1:2,AF: FC=1:1,AE与BF相交于点G、现作EH ∥BF交AC于点H、依次求FH ：HC、AG： GE、BG：GF的值
(3)如图3，△ABC中，点P在边AB上，点M、N在边AC上，且有AP=PB,AM=MN=NC，BM、BW与CP分别相交于点R、Q.,现已知△ABC的面积为1，求△BRQ的面积。
【答案】（1）1：3；（2）
、
、
；（3）
.
【解析】试题分析：根据两个三角形有一个相同的高，它们的面积之比等于相应的底之比进行计算即可；
（2）由平行线分线段成比例定理即可得解；
（3）由（2）易得
、
、
，因△ABC的面积为1．则可得： 
， 
．
试题解析：（1）
=
=
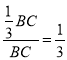
（2）
、
、
（3）由（2）易得： 
、
、
△ABC的面积为1．则
， 
．
练习册系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
