Question

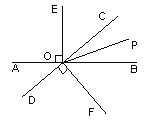
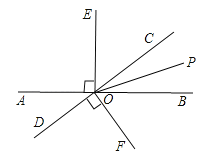
【题目】如图，直线AB与CD相交于点O，OE⊥AB，OF⊥CD，OP是∠BOC的平分线.

（1）请写出图中所有∠EOC的补角 ____________________；

（2）如果∠POC：∠EOC＝2：5．求∠BOF的度数.

Answer 1

【答案】（1）∠EOD和∠AOF；（2）50°.

【解析】试题分析：（1）首先根据垂直定义可得∠AOE=∠DOF=90°，然后再证明∠EOD=∠AOF，根据补角定义可得∠EOD，∠AOF都是∠EOC的补角；

（2）根据角平分线定义可得∠POC=∠POB，再根据条件∠POC：∠EOC=2：5，可得∠COP的度数，然后即可算出∠BOF的度数．

试题解析：解：（1）∵OE⊥AB，OF⊥CD，∴∠AOE=∠DOF=90°，∴∠EOA+∠AOD=∠DOF+∠AOD，即：∠EOD=∠AOF，∵∠EOC+∠EOD=180°，∴∠AOF+∠EOC=180°，∴∠EOD，∠AOF都是∠EOC的补角，故答案为：∠EOD，∠AOF；

（2）∵OP是∠BOC的平分线，∴∠POC=∠POB，∵∠POC：∠EOC=2：5，∴∠POC=90°×=20°，∴∠POB=20°，∵∠DOF=90°，∴∠BOF=90°﹣20°﹣20°=50°．