题目内容
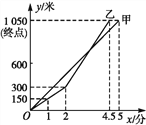
【题目】某公司投资1200万元购买了一条新生产线生产新产品.根据市场调研,生产每件产品需要成本50元,该产品进入市场后不得低于80元/件且不得超过160元/件,该产品销售量y(万件)与产品售价x(元)之间的关系如图所示.
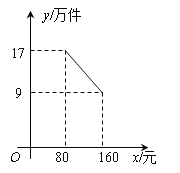
(1)求y与x之间的函数关系式,并写出x的取值范围;
(2)第一年公司是盈利还是亏损?求出当盈利最大或亏损最小时的产品售价;
(3)在(2)的前提下,即在第一年盈利最大或者亏损最小时,公司第二年重新确定产品售价,能否使前两年盈利总额达790万元?若能,求出第二年产品售价;若不能,说明理由.
【答案】(1)![]() x的取值范围是80≤x≤160;(2)第一年公司是亏损,且当亏损最小时的产品售价为150元/件;(3)第二年售价是140元/件或160/件.
x的取值范围是80≤x≤160;(2)第一年公司是亏损,且当亏损最小时的产品售价为150元/件;(3)第二年售价是140元/件或160/件.
【解析】试题分析:(1)设y=kx+b,则由图象可求得k,b,从而得出y与x之间的函数关系式,并写出x的取值范围80≤x≤160;
(2)设公司第一年获利W万元,则可表示出W=﹣![]() (x﹣180)2﹣60≤﹣60,则第一年公司亏损了,当产品售价定为180元/件时,亏损最小,最小亏损为60万元;
(x﹣180)2﹣60≤﹣60,则第一年公司亏损了,当产品售价定为180元/件时,亏损最小,最小亏损为60万元;
(3)假设两年共盈利1340万元,则﹣![]() x2+36x﹣1800﹣60=1340,解得x的值,根据100≤x≤180,则x=160时,公司两年共盈利达1340万元.
x2+36x﹣1800﹣60=1340,解得x的值,根据100≤x≤180,则x=160时,公司两年共盈利达1340万元.
解:(1)设y=kx+b.由图象可得:![]() ,
,
解得: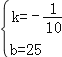 .
.
所以y=﹣![]() x+25,
x+25,
故x的取值范围是80≤x≤160.
(2)设该公司第一年获利S万元,则
S=(x﹣50)×y﹣1200=(x﹣50)(﹣![]() x+25)﹣1200
x+25)﹣1200
=﹣![]() x2+30x﹣2450
x2+30x﹣2450
=﹣![]() (x﹣150)2﹣200≤﹣200,
(x﹣150)2﹣200≤﹣200,
所以第一年公司是亏损,且当亏损最小时的产品售价为150元/件.
(3)由题意可列方程(x﹣50)(﹣![]() x+25)+(﹣200)=790,
x+25)+(﹣200)=790,
解得:x1=140,x2=160.
两个x的值都在80≤x≤160内,
所以第二年售价是140元/件或160/件.

【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
y | … | ﹣6 | 0 | 4 | 6 | 6 | … |
给出下列说法:
①抛物线与y轴的交点为(0,6);
②抛物线的对称轴在y轴的左侧;
③抛物线一定经过(3,0)点;
④在对称轴左侧y随x的增大而减增大.
从表中可知,其中正确的个数为( )
A.4 B.3 C.2 D.1