题目内容
如图,已知边长为4的正方形ABCD,E是BC边上一动点(与B、C不重合),连结AE,作EF⊥AE交∠BCD的外角平分线于F,设BE=x,△ECF的面积为y,下列图象中,能表示y与x的函数关系的图象大致是( )
A. B.
B.
C. D.
D.
B.
解析试题分析:如图,过点E作EH⊥BC于点H,
∵四边形ABCD是正方形,∴∠DCH=90°.
∵CE平分∠DCH,∴∠ECH=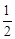 ∠DCH=45°.
∠DCH=45°.
∵∠H=90°,∴∠ECH=∠CEH=45°.∴EH=CH.
∵四边形ABCD是正方形,AP⊥EP,∴∠B=∠H=∠APE=90°.
∴∠BAP+∠APB=90°,∠APB+∠EPH=90°.∴∠BAP=∠EPH.
∵∠B=∠H=90°,∴△BAP∽△HPE. ∴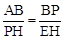 ,即
,即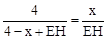 .∴EH=x.
.∴EH=x.
∴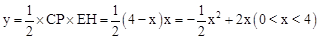 ,它的图象是抛物线的一部分.
,它的图象是抛物线的一部分.
故选B.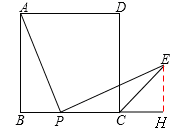
考点:1.单动点问题;2.由实际问题列函数关系式;3.正方形的性质;4.相似三角形的判定和性质.

练习册系列答案
相关题目
如图,二次函数y=ax2+bx+c的图象经过(-1,0)、(0,3),下列结论中错误的是( )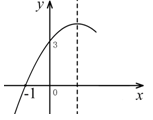
| A.abc<0 | B.9a+3b+c=0 | C.a-b="-3" | D. 4ac﹣b2<0 |
函数 与
与 在同一直角坐标系中的图象可能是( )
在同一直角坐标系中的图象可能是( )
A. | B. | C. | D. |
若二次函数y=x2﹣2x+c的图象与y轴的交点为(0,﹣3),则此二次函数有( )
| A.最小值为-2 | B.最小值为-3 | C.最小值为-4 | D.最大值为-4 |
对于二次函数y=2(x+1)(x-3),下列说法正确的是( )
| A.图象的开口向下 |
| B.当x>1时,y随x的增大而减小 |
| C.当x<1时,y随x的增大而减小 |
| D.图象的对称轴是直线x=-1 |
如图,抛物线y=ax2+bx+c与x轴交于点(1,0),对称轴为x=1,则下列结论中正确的是( )
A. |
B.当 时,y随x的增大而增大 时,y随x的增大而增大 |
C. |
D. 是一元二次方程 是一元二次方程 的一个根 的一个根 |
将函数 变形为
变形为 的形式,正确的是( )
的形式,正确的是( )
A. | B. |
C. | D. |
已知二次函数y=a(x+1)2-b(a≠0)有最小值,则a,b的大小关系为 ( )
| A.a>b | B.a<b |
| C.a=b | D.不能确定 |