题目内容
【题目】如图,锐角三角形ABC中(AB>AC),AH⊥BC,垂足为H,E、D、F分别是各边的中点,则四边形EDHF是( ) 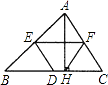
A.梯形
B.等腰梯形
C.直角梯形
D.矩形
【答案】B
【解析】解:∵E、D、F分别是各边的中点.∴ED∥AC,ED= ![]() AC=FC,EF∥BC,EF=
AC=FC,EF∥BC,EF= ![]() BC=DC.
BC=DC.
∴四边形EFCD是平行四边形.
∴DE=CF.
∵AH⊥BC,垂足为H,F是AC的中点.
∴HF= ![]() AC=CF.
AC=CF.
∴HF=DE.
∵DH∥EF.
∴四边形EDHF是等腰梯形.
故选B.
【考点精析】掌握三角形中位线定理和等腰梯形的判定是解答本题的根本,需要知道连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半;两腰相等的梯形是等腰梯形;同一底上的两个角相等的梯形是等腰梯形;两条对角线相等的梯形是等腰梯形.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目