题目内容
现有四种地面砖,它们的形状分别是:正三角形、正方形、正六边形、正八边形,且它们的边长都相等.同时选择其中两种地面砖密铺地面,选择的方式有( )
| A.2种 | B.3种 | C.4种 | D.5种 |
B
本题考查镶嵌问题、多边形的内角和、二元一次方程整数解的问题
本题要先计算出各类正多边形每个内角的度数,然后利用二元一次方程的正整数解来解决.如用x个正三角形和y个正四边形来密铺,则60x+90y=360,有正整数解:x=3,y=2,故可以实现密铺,同样正三角形与正六边形,正方形与正八边形也可以组合在一起实现密铺,其它组合则实现不了密铺,因此选B.解决此题学生容易由于审题不清,误以为这四种地面砖单独使用而误选C.
设用x个正三角形和y个正四边形来密铺,则60x+90y=360,有正整数解:x=3,y=2,故可以实现密铺,
同理可知正三角形与正六边形,正方形与正八边形.
所以可以密铺的两种地面砖有:正三角形和正四边形;正三角形与正六边形;正方形与正八边形,共3种.
故选B
本题要先计算出各类正多边形每个内角的度数,然后利用二元一次方程的正整数解来解决.如用x个正三角形和y个正四边形来密铺,则60x+90y=360,有正整数解:x=3,y=2,故可以实现密铺,同样正三角形与正六边形,正方形与正八边形也可以组合在一起实现密铺,其它组合则实现不了密铺,因此选B.解决此题学生容易由于审题不清,误以为这四种地面砖单独使用而误选C.
设用x个正三角形和y个正四边形来密铺,则60x+90y=360,有正整数解:x=3,y=2,故可以实现密铺,
同理可知正三角形与正六边形,正方形与正八边形.
所以可以密铺的两种地面砖有:正三角形和正四边形;正三角形与正六边形;正方形与正八边形,共3种.
故选B

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
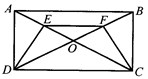
 中,
中, 是
是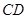 边上的中点,
边上的中点, 与
与 相交于点
相交于点 ,连接
,连接 .(注:正方形的四边相等,四个角都是直角,每一条对角线平分一组对角).
.(注:正方形的四边相等,四个角都是直角,每一条对角线平分一组对角). 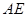 试判断
试判断 于点
于点 ,试判断
,试判断 与
与 的数量关系,并说明理由.
的数量关系,并说明理由.