题目内容
如图是某地下商业街的入口,数学课外兴趣小组同学打算运用所学知识测量侧面支架最高点E到地面距离EF.经测量,支架立柱BC与地面垂直,即∠BCA=90°,且BC=1.5cm,点F、A、C在同一条水平线上,斜杆AB与水平线AC夹角∠BAC=30°,支撑杆DE⊥AB于点D,该支架边BE与AB夹角∠EBD=60°,又测得AD=1m。请你求出该支架边BE及顶端E到地面距离EF长度。


EB=4m EF= 3.5(m)
分析:过B作BH⊥EF于点H,在Rt△ABC中,根据∠BAC=30°,BC=1.5,可求得AB的长度,又AD=1m,可求得BD的长度,在Rt△EBD中解直角三角形求得EB的长度,然后根据BH⊥EF,求得∠EBH=30°,继而可求得EH的长度,易得EF=EH+HF的值。
解:过B作BH⊥EF于点H,
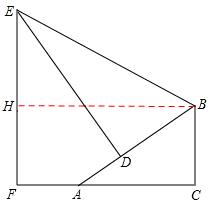
∴四边形BCFH为矩形,BC=HF=1.5m,∠HBA=∠AC=30°。
在Rt△ABC中,∵∠BAC=30°,BC=1.5m,∴AB=3m。
∵AD=1m,∴BD=2m。
在Rt△EDB中,∵∠EBD=60°,∴∠BED=90°-60°=30°。
∴EB=2BD=2×2=4m。
又∵∠HBA=∠BAC=30°,∴∠EBH=∠EBD--∠HBD=30°,
∴EH=
 EB=2m。
EB=2m。∴EF=EH+HF=2+1.5=3.5(m)。
答:该支架的边BE为4m,顶端E到地面的距离EF的长度为3.5m.

练习册系列答案
相关题目

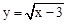 的自变量x的取值范围是x>3
的自变量x的取值范围是x>3  .
.
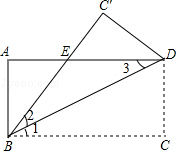
 中,
中, ,
, 为垂足,如果
为垂足,如果 ,则
,则 的度数是______________.
的度数是______________.

