题目内容
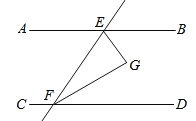
【题目】如图1,AB//EF,∠2=2∠1

(1)证明∠FEC=∠FCE;
(2)如图2,M为AC上一点,N为FE延长线上一点,且∠FNM=∠FMN,则∠NMC与∠CFM有何数量关系,并证明.
【答案】(1)见解析;(2)∠CFM=2∠NMC,理由见解析
【解析】
(1)由平行线的性质可得∠1=∠CEF,再加上∠2=2∠1,∠2=∠CEF+∠C,从而得到结论;
(2)如图,由三角形外角性质可得∠7=∠3+∠4,从而得到∠C=∠3+∠4,再加上∠C+∠5=∠8+∠N可得∠3+∠4+∠5=∠8+∠N,再加上∠FNM=∠FMN可得:∠3+∠4+∠5=∠8+∠3+∠8,从而得出结论.
(1)∵AB//EF,
∴∠1=∠CEF,
又∵∠2=2∠1(已知),∠2=∠CEF+∠C(三角形外角的性质),
∴2∠1=∠2=∠1+∠C,
∴∠1=∠C,
∴∠FEC=∠C,即∠FEC=∠FCE;
(2)如图所示:
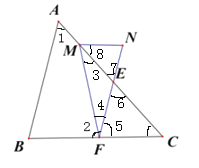
∵∠7=∠3+∠4,∠7=∠6,∠6=∠C(已证),
∴∠C=∠3+∠4,
又∵∠7=∠6,
∴∠C+∠5=∠8+∠N,
∴∠3+∠4+∠5=∠8+∠N,
又∵∠FNM=∠FMN,
∴∠N=∠3+∠8,
∴∠3+∠4+∠5=∠8+∠3+∠8,
又∵∠4+∠5=∠CFM,
∴∠3+∠CFM=∠8+∠3+∠8,
∴∠CFM=2∠8,即∠CFM=2∠NMC.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目