题目内容
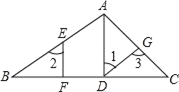
【题目】如图,△ABC为等边三角形,AB=8,AD⊥BC,点E为线段AD上的动点,连接CE,以CE为边作等边△CEF,连接DF,则线段DF的最小值为( )

A.![]() B.4C.2D.无法确定
B.4C.2D.无法确定
【答案】C
【解析】
连接BF,由等边三角形的性质可得三角形全等的条件,从而可证△BCF≌△ACE,推出∠CBF=∠CAE=30°,再由垂线段最短可知当DF⊥BF时,DF值最小,利用含30°的直角三角形的性质定理可求DF的值.
如图,连接BF,
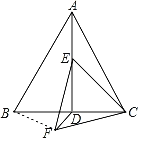
∵△ABC为等边三角形,AD⊥BC,AB=8,
∴BC=AC=AB=8,BD=DC=4,∠BAC=∠ACB=60°,∠CAE=30°,
∵△CEF为等边三角形,
∴CF=CE,∠FCE=60°,
∴∠FCE=∠ACB,
∴∠BCF=∠ACE,
∴在△BCF和△ACE中,
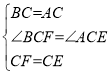 ,
,
∴△BCF≌△ACE(SAS),
∴∠CBF=∠CAE=30°,AE=BF,
∴当DF⊥BF时,DF值最小,
此时∠BFD=90°,∠CBF=30°,BD=4,
∴DF=2,
故选:C.

练习册系列答案
相关题目