题目内容
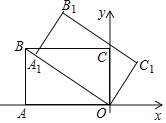
【题目】已知一次函数y=x+2的图象分别交x轴，y轴于A、B两点，⊙O1过以OB为边长的正方形OBCD的四个顶点，两动点P、Q同时从点A出发在四边形ABCD上运动，其中动点P以每秒
个单位长度的速度沿A→B→A运动后停止；动点Q以每秒2个单位长度的速度沿A→O→D→C→B运动，AO1交y轴于E点，P、Q运动的时间为t（秒）．
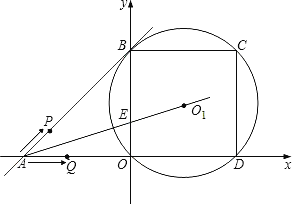
（1）求E点的坐标和S△ABE的值；
（2）试探究点P、Q从开始运动到停止，直线PQ与⊙O1有哪几种位置关系，并求出对应的运动时间t的范围．
【答案】（1）E（0，
），
；（2）当PQ与⊙O1相离，0＜t＜1；当PQ与⊙O1相切时，t=1或t=4；当PQ与⊙O1相交时，4＞t＞1.
【解析】
（1）依题意容易知道O1的坐标，根据待定系数法可以确定直线AE的解析式，然后求出E的坐标，最后求出S△ABE；
（2）容易知道当Q运动到O点时PQ与圆相切，此时t=1，所以可以确定其他位置的t的值；
（1）由题意知，A（﹣2，0），B（0，2），
∴OB=OD=2，∴O1（1，1），
设AO1的直线的解析式为y=kx+b，则有0=﹣2k+b，1=k+b，
解得：b=，k=
，
∴y=x+，∴E（0，），
∴BE=，S△ABE=
OABE=；
（2）直线PQ与⊙O1有三种位置关系，分别是相离，相切，相交，
∵动点P沿A→B→A运动后停止；动点Q沿A→O→D→C→B运动，
∴根据切线的定义，如果PQ与⊙O1相切，切点只能是O、D、C、B中的一个.
分两种情况：
①当点P从A点移到B点时，由于OA=OB=2,
∴AB=
，
∴t=
=2，
当t=2时，点Q从A点运动到D点，
当到达D点时，点P在B点，显然不合题意，舍去，
当点Q在O点时，如图①，此时t=2
,连结O1Q、PQ,易知PA=
,
∵QA=QB,
∴∠PQB=
,
∵O1是正方形ODCB的中心，
∴∠O1QB=
,
∴∠PQO1=900,
∴PQ为⊙O1的切线，此时t=1
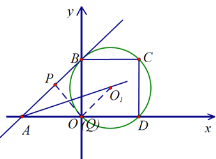
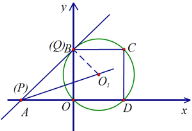
图① 图②
②当点P从B点移到A点时, 点Q从D点经过C点到达B点，显然，当点Q在点C处时，PQ与⊙O1相交，当点Q运动到B点时，点P回到了点A,如图②，同理可证此时PQ与⊙O1相切，易得t=4，
综上，当t=1或t=4时，PQ与⊙O1相切，
∴由题意可知：
当PQ与⊙O1相离，0＜t＜1；
当PQ与⊙O1相切时，t=1或t=4；
当PQ与⊙O1相交时，4＞t＞1；
