题目内容
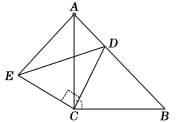
【题目】如图,AB是⊙O的直径,AC是⊙O的切线,切点为A,BC交⊙O于点D,点E是AC的中点.
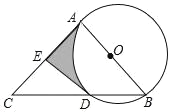
(1)试判断直线DE与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为2,∠B=45°,AC=4,求图中阴影部分的面积.
【答案】(1)见解析;(2)4π
【解析】
(1)根据切线的定义可知∠CAB=90°,有圆周角定理可知∠ADB=90°,E为斜边中点
(2)阴影部分的面积等于正方形AEDO的面积减去扇形AOD的面积.
(1)如图,连接AD,OD
∵AB是直径
∴∠ADB=90°
∴∠OAD=∠ODA,∠ODB=∠OBD
∠ADE=∠EAD,∠EDC=∠ECD
∵∠EAD+∠OAD=90°
∴∠ADE+∠ODA=90°
∴直线DE与⊙O相切
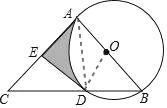
(2)由(1)可知△ACD与△ADB是直角三角形
若∠B=45°,则AC=AB=4,AE=EC=AO=DO=BO=2
∴四边形AEDO为正方形
阴影面积=正方形AEDO扇形AOD=![]() =4π
=4π

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目