题目内容
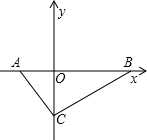
 在直角坐标平面中,O为坐标原点,二次函数y=x2+bx+c的图象与y轴的负半轴相交于点C(如图),点C的坐标为(0,-3),且BO=CO.
在直角坐标平面中,O为坐标原点,二次函数y=x2+bx+c的图象与y轴的负半轴相交于点C(如图),点C的坐标为(0,-3),且BO=CO.(1)求出B点坐标和这个二次函数的解析式;
(2)求△ABC的面积;
(3)若P是抛物线对称轴上一个动点,求当PA+PC的值最小时P点坐标.
分析:(1)由BO=CO及点C的坐标为(0,-3),就可以求出B的坐标,再把B、C的坐标代入解析式就可以求出二次函数的解析式;
(2)当y=0时求出x的值,就可以求出A点的坐标,从而求出AB的长,OC是高就可以求出三角形ABC的面积.
(3)根据轴对称的性质及抛物线的图象特征可以得出A点关于抛物线对称轴的对称点是B点.连接BC与对称轴的交点就是P点,求出BC的解析式,把对称轴的横坐标代入直线的解析式就可以求出P点的坐标.
(2)当y=0时求出x的值,就可以求出A点的坐标,从而求出AB的长,OC是高就可以求出三角形ABC的面积.
(3)根据轴对称的性质及抛物线的图象特征可以得出A点关于抛物线对称轴的对称点是B点.连接BC与对称轴的交点就是P点,求出BC的解析式,把对称轴的横坐标代入直线的解析式就可以求出P点的坐标.
解答:解:(1)∵点C的坐标为(0,-3),
∴OC=3,
∵BO=CO,
∴OB=3,
∴B(3,0),
∴
,
解得:
,
∴二次函数的解析式为:y=x2-2x-3;
(2)∵二次函数的解析式为:y=x2-2x-3,
∴当y=0时,x1=-1,x2=3,
∴AB=4,
S△ABC=
=6;
(3)由抛物线的对称性可以得出点A、B关于抛物线的对称轴对称,
∴连接BC交对称轴于点P,则点P是所求的点,
∵y=x2-2x-3,
∴y=(x-1)2-4,
∴对称轴为:x=1,
∴P点的横坐标为1,设直线BC的解析式为:y=kx+b,则
,
解得;
,
∴直线BC的解析式为:y=x-3,
∴x=1,时,y=-2,
∴P(1,-2).

∴OC=3,
∵BO=CO,
∴OB=3,
∴B(3,0),
∴
|
解得:
|
∴二次函数的解析式为:y=x2-2x-3;
(2)∵二次函数的解析式为:y=x2-2x-3,
∴当y=0时,x1=-1,x2=3,
∴AB=4,
S△ABC=
| 4×3 |
| 2 |
(3)由抛物线的对称性可以得出点A、B关于抛物线的对称轴对称,
∴连接BC交对称轴于点P,则点P是所求的点,
∵y=x2-2x-3,
∴y=(x-1)2-4,
∴对称轴为:x=1,
∴P点的横坐标为1,设直线BC的解析式为:y=kx+b,则
|
解得;
|
∴直线BC的解析式为:y=x-3,
∴x=1,时,y=-2,
∴P(1,-2).

点评:本题是一道二次函数的综合试题,考查了运用待定系数法求函数的解析式,三角形的面积,轴对称,最短路线问题.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
 如图,在直角坐标平面中,Rt△ABC的斜边AB在x轴上,直角顶点C在y轴的负半轴上,cos∠ABC=
如图,在直角坐标平面中,Rt△ABC的斜边AB在x轴上,直角顶点C在y轴的负半轴上,cos∠ABC= (2012•长宁区二模)如图,在直角坐标平面中,等腰△ABC的顶点A在第一象限,B(2,0),C(4,0),△ABC的面积是3.
(2012•长宁区二模)如图,在直角坐标平面中,等腰△ABC的顶点A在第一象限,B(2,0),C(4,0),△ABC的面积是3.