题目内容
 (2012•长宁区二模)如图,在直角坐标平面中,等腰△ABC的顶点A在第一象限,B(2,0),C(4,0),△ABC的面积是3.
(2012•长宁区二模)如图,在直角坐标平面中,等腰△ABC的顶点A在第一象限,B(2,0),C(4,0),△ABC的面积是3.(1)若x轴表示水平方向,设从原点O观测点A的仰角为α,求tanα的值;
(2)求过O、A、C三点的抛物线解析式,并写出抛物线的对称轴和顶点坐标.
分析:(1)作AH⊥BC,垂足为H,由B、C两点坐标及△ABC是等腰三角形,可求OH,再由△ABC的面积求AH,根据正切的定义求tanα的值;
(2)根据抛物线过O(0,0),设抛物线解析式为y=ax2+bx,将A、C两点坐标代入,列方程组求a、b的值,确定抛物线解析式,根据抛物线解析式求抛物线的对称轴和顶点坐标.
(2)根据抛物线过O(0,0),设抛物线解析式为y=ax2+bx,将A、C两点坐标代入,列方程组求a、b的值,确定抛物线解析式,根据抛物线解析式求抛物线的对称轴和顶点坐标.
解答:解:(1)作AH⊥BC,垂足为H,
∵△ABC是等腰三角形,∴H是BC中点,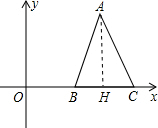
∵B(2,0),C(4,0)
∴H(3,0),BC=2,
S△ABC=
BC•AH=3,∴AH=3,A(3,3),
tanα=
=1;
(2)据题意,设抛物线解析式为y=ax2+bx(a≠0)
A(3,3),C(4,0)代入得
,
解得
,
所求解析式为y=-x2+4x,
对称轴直线 x=2,顶点(2,4).
∵△ABC是等腰三角形,∴H是BC中点,

∵B(2,0),C(4,0)
∴H(3,0),BC=2,
S△ABC=
| 1 |
| 2 |
tanα=
| AH |
| OH |
(2)据题意,设抛物线解析式为y=ax2+bx(a≠0)
A(3,3),C(4,0)代入得
|
解得
|
所求解析式为y=-x2+4x,
对称轴直线 x=2,顶点(2,4).
点评:本题考查了待定系数法求二次函数解析式,二次函数的性质,等腰三角形的性质,锐角三角函数的定义.关键是明确锐角三角函数的定义,待定系数法求抛物线解析式的一般方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目