Question

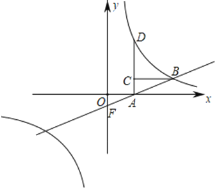
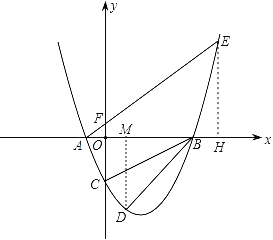
【题目】如图，设抛物线y＝ax2+bx+c与x轴交于两个不同的点A（﹣1，0），B（m，0），与y轴交于点C（0，﹣2），且∠ACB＝90度．

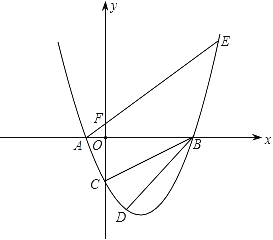
（1）求m的值和抛物线的解析式；

（2）已知点D（1，n）在抛物线上，过点A的直线y＝x+1交抛物线于另一点E，求点D和点E的坐标；

（3）在x轴上是否存在点P，使以点P，B，D为顶点的三角形与三角形AEB相似？若存在，请求出点P的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）m＝4，y＝x2﹣x﹣2；（2）D（1，﹣3），E（6，7）；（3）在x轴上存在点P1（，0），P2（﹣，0）满足条件．

【解析】

（1）利用 结合相似三角形的性质得从而求解的值，利用待定系数法求二次函数的解析式，

（2）把点D（1，n）代入函数解析式可得D的坐标，联立一次函数与二次函数解析式解方程组可得E的坐标，

（3）作EH⊥x轴于点H，作DM⊥x轴于点M，利用点的坐标得到∠EAB＝∠DBP＝45°，再分两种情况讨论即可得到答案．

解：（1）在直角△ABC中，

∵CO⊥AB

∴

∴22＝1×m，即m＝4

∴B（4，0）．

把A（﹣1，0）B（4，0）分别代入y＝ax2+bx﹣2，

解方程组得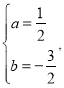

∴

（2）把D（1，n）代入

得n＝﹣3，

∴D（1，﹣3）

解方程组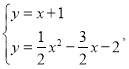

得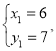

∴E（6，7）．

（3）作EH⊥x轴于点H，则EH＝AH＝7，

∴∠EAB＝45°，

由勾股定理得：BE＝ AE＝

作DM⊥x轴于点M，D（1，﹣3）

则DM＝BM＝3，

∴∠DBM＝45°

由勾股定理得BD＝

假设在x轴上存在点P满足条件，

∵∠EAB＝∠DBP＝45°，

∴当 时，

当时，

即

∴

在轴的负半轴上，

∴在x轴上存在点或满足条件．