Question

【题目】已知在平面直角坐标中，点在第一象限内，且，反比例函数的图像经过点，

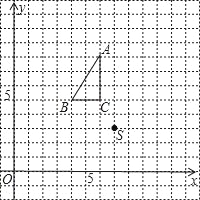
（1）当点的坐标为时（如图），求这个反比例函数的解析式；

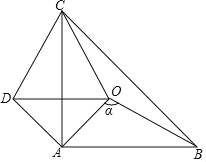
（2）当点在反比例函数的图像上，且在点的右侧时（如图2），用含字母的代数式表示点的坐标；

（3）在第（2）小题的条件下，求的值。

Answer 1

【答案】（1）（2）（3）

【解析】

（1）过A作AC⊥OB，根据三角形AOB为等腰直角三角形，得到AC=OC=BC=OB，确定出A坐标，代入反比例解析式求出k的值，即可确定出反比例解析式；
（2）过A作AE⊥x轴，过B作BD⊥AE，利用同角的余角相等得到一对角相等，再由一对直角相等，且AO=AB，利用AAS得出三角形AOE与三角形ABD全等，由确定三角形的对应边相等得到BD=AE=n，AD=OE=m，进而表示出ED及OE+BD的长，即可表示出B坐标；
（3）由A与B都在反比例图象上，得到A与B横纵坐标乘积相等，列出关系式，变形后即可求出的值．

解：（1）如图1，过A作AC⊥OB，交x轴于点C，

∵OA=AB，∠OAB=90°，
∴△AOB为等腰直角三角形，
∴AC=OC=BC=OB=3，
∴A（3，3），
将x=3，y=3代入反比例解析式得：3= ，即k=9，
则反比例解析式为y=；

（2）如图2，过A作AE⊥x轴，过B作BD⊥AE，
∵∠OAB=90°，
∴∠OAE+∠BAD=90°，
∵∠AOE+∠OAE=90°，
∴∠BAD=∠AOE，
在△AOE和△BAD中，

∴△AOE≌△BAD（AAS），
∴AE=BD=n，OE=AD=m，
∴DE=AE-AD=n-m，OE+BD=m+n，
则B（m+n，n-m）；

（3）由A与B都在反比例图象上，得到mn=（m+n）（n-m），
整理得：n2-m2=mn，即（）2+-1=0，
这里a=1，b=1，c=-1，
∵△=1+4=5，
∴= ，
∵A（m，n）在第一象限，
∴m＞0，n＞0，
则=．