题目内容
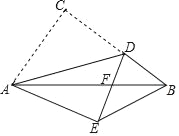
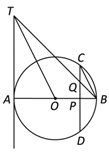
【题目】如图,在△ABC中,AD平分∠BAC交BC于点D,DE⊥AB于点E,DF⊥AC于点F,∠MDN的两边分别与AB,AC相交于M,N两点,且∠MDN+∠BAC=180°.
(1)求证AE=AF;
(2)若AD=6,DF=2![]() ,求四边形AMDN的面积.
,求四边形AMDN的面积.

【答案】(1)详见解析;(2)![]()
【解析】
(1)依据HL判定Rt△ADE≌Rt△ADF,即可得出AE=AF;
(2)判定△DEM≌△DFN,可得S△DEM=S△DFN,进而得到S四边形AMDN=S四边形AEDF,求得S△ADF=![]() AF×DF=2
AF×DF=2![]() ,即可得出结论.
,即可得出结论.
(1)∵AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,
∴DE=DF,
又∵DE⊥AB于点E,DF⊥AC于点F,
∴∠AED=∠AFD=90°,
又∵AD=AD,
∴Rt△ADE≌Rt△ADF(HL),
∴AE=AF;
(2)∵∠MDN+∠BAC=180°,
∴∠AMD+∠AND=180°,
又∵∠DNF+∠AND=180°
∴∠EMD=∠FND,
又∵∠DEM=∠DFN,DE=DF,
∴△DEM≌△DFN,
∴S△DEM=S△DFN,
∴S四边形AMDN=S四边形AEDF,
∵AD=6,DF=2![]() ,
,
∴Rt△ADF中,AF=![]()
∴![]()
∴![]()
![]()

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目