题目内容
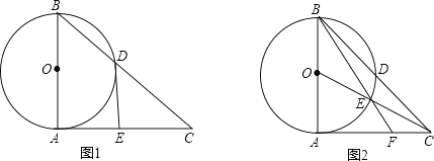
【题目】以△ABC的边AB为直径作⊙O交BC于D.
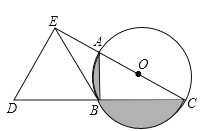
(1)如图1,过点D作⊙O的切线交AC于E,若点E为线段AC中点,求证:AC与⊙O相切.
(2)在(1)的条件下,若BD=6,AB=10,求△ABC的面积.
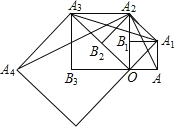
(3)如图2,连OC交⊙O于E,BE的延长线交AC于F,若AB=AC,CE=AF=4,求CF的长.
【答案】(1)见解析;(2)![]() ;(3)CF=
;(3)CF=![]()
【解析】
(1)连接OD,OE,利用全等三角形的判定得出△ODE与△OAE全等,再利用切线的判定证明即可;
(2)根据切线的性质和勾股定理和三角形面积公式解答即可.
(3)由△AEC∽△EFC即可得出FC的长.
证明:(1)连接OD,OE,AD,
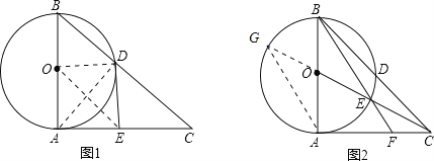
∵AB为直径,
∴∠ADB=90°,
∴∠ADC=90°,
∵点E为线段AC中点,
∴AE=EC,
∴AE=DE,
在△ODE与△OAE中
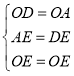 ,
,
∴△ODE≌△OAE(SSS),
∴∠ODE=∠OAE,
∵⊙O的切线交AC于E,
∴∠ODE=90°,
∴∠OAE=90°,
∴OA⊥AC,
即AC与⊙O相切;
(2)如图3,连接AD,AE
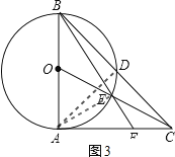
∵△ABD∽△ADC
∴![]() =
=![]() =
=![]()
∴![]() =
=![]() =
=![]()
∴CD=![]() ,AC=
,AC=![]()
∴S△ABC=![]() =
=![]() =
=![]() ;
;
(3)如图,作FH∥AB交OC于H,设半径为r
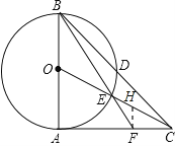
△FEH为等腰三角形
∵AC=AB=2r
∴CF=2r-4
∵△CFH∽△OAC
∴![]()
∴HF=r-2
∴EH=r-2
∴HC=4-(r-2)=6-r
∵△CFH∽△OAC
∴![]()
∴![]()
∴r=1±![]()
∴r=1+![]()
∴CF=2r-4=2![]() -2.
-2.

 全能测控一本好卷系列答案
全能测控一本好卷系列答案【题目】某公司计划从甲、乙两种产品中选择一种生产并销售,每年产销x件.已知产销两种产品的有关信息如下表:
产品 | 每件售价(万元) | 每件成本(万元) | 每年其他费用(万元) | 每年最大产销量(万元) |
甲 | 10 | a | 40 | 200 |
乙 | 18 | 8 | 40+0.05x2 | 100 |
其中a为常数,且5≤a≤8.
(1)若产销甲、乙两种产品的年利润分别为y1万元、y2万元,直接写出y1、y2与x的函数关系式;
(2)分别求出产销两种产品的最大年利润;
(3)为获得最大年利润,该公司应该选择产销哪种产品?请说明理由.
【题目】某工厂计划生产![]() ,
,![]() 两种产品共10件,其生产成本和利润如下表.
两种产品共10件,其生产成本和利润如下表.
|
| |
成本(万元 | 2 | 5 |
利润(万元 | 1 | 3 |
(1)若工厂计划获利14万元,问![]() ,
,![]() 两种产品应分别生产多少件?
两种产品应分别生产多少件?
(2)若工厂计划投入资金不多于44万元,且获利多于22万元,问工厂有哪几种生产方案?