题目内容
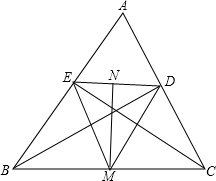 已知BD,CE是△ABC的两条高,M、N分别为BC、DE的中点,勇敢猜一猜:
已知BD,CE是△ABC的两条高,M、N分别为BC、DE的中点,勇敢猜一猜:(1)线段EM与DM的大小有什么关系?
(2)线段MN与DE的位置有什么关系?
分析:(1)根据直角三角形斜边上的中线等于斜边的一半即可证明;
(2)结合(1)的结论,根据等腰三角形的三线合一即可得出结论.
(2)结合(1)的结论,根据等腰三角形的三线合一即可得出结论.
解答:解:(1)EM=DM.理由如下:
∵在直角三角形BCE和直角三角形BCD中,BM=CM.
∴EM=
BC,DM=
BC(直角三角形斜边上的中线等于斜边的一半),
∴EM=DM;
(2)MN⊥DE.
理由如下:
∵EM=DM,EN=DN,
∴MN⊥DE(三线合一).
∵在直角三角形BCE和直角三角形BCD中,BM=CM.
∴EM=
| 1 |
| 2 |
| 1 |
| 2 |
∴EM=DM;
(2)MN⊥DE.
理由如下:
∵EM=DM,EN=DN,
∴MN⊥DE(三线合一).
点评:此题综合运用了直角三角形和等腰三角形的性质,此题的中点比较多,要充分发挥其作用.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
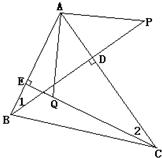 25、已知BD、CE是△ABC的高,点P在BD的延长线上,BP=AC,点Q在CE上,CQ=AB.判断线段AP和AQ的关系,并证明.
25、已知BD、CE是△ABC的高,点P在BD的延长线上,BP=AC,点Q在CE上,CQ=AB.判断线段AP和AQ的关系,并证明.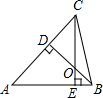 已知BD、CE是△ABC的高,∠A=50°,直线BD、CE相交于点O,则∠BOC=
已知BD、CE是△ABC的高,∠A=50°,直线BD、CE相交于点O,则∠BOC=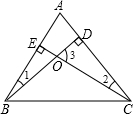 如图,已知BD、CE是△ABC的高,下面给出四个结论:①∠1=∠2=90°-∠A;②∠3=∠A=90°-∠1;③∠BOC=∠A+∠1+∠2;④∠1+∠2+∠3+∠A=180°,其中正确的个数是( )
如图,已知BD、CE是△ABC的高,下面给出四个结论:①∠1=∠2=90°-∠A;②∠3=∠A=90°-∠1;③∠BOC=∠A+∠1+∠2;④∠1+∠2+∠3+∠A=180°,其中正确的个数是( )