题目内容
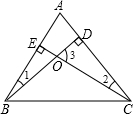 如图,已知BD、CE是△ABC的高,下面给出四个结论:①∠1=∠2=90°-∠A;②∠3=∠A=90°-∠1;③∠BOC=∠A+∠1+∠2;④∠1+∠2+∠3+∠A=180°,其中正确的个数是( )
如图,已知BD、CE是△ABC的高,下面给出四个结论:①∠1=∠2=90°-∠A;②∠3=∠A=90°-∠1;③∠BOC=∠A+∠1+∠2;④∠1+∠2+∠3+∠A=180°,其中正确的个数是( )分析:根据三角形内角和定理为180°以及三角形外角性质,分别求出即可.
解答: 解:∵BD,CE是△ABC的高,
解:∵BD,CE是△ABC的高,
∴∠AEC=90°,∠BDA=90°,
∴∠1+∠A=90°,∠2+∠A=90°,
∴∠1=∠2=90°-∠A,
故①正确;
∵∠ODC=90°,
∴∠3+∠2=90°,
∴∠3=90°-∠2,
∵∠2=90°-∠A,
∴∠A=90°-∠2,
∴∠3=∠A=90°-∠1,
故②正确;
∵∠BDC=∠A+∠1,∠BOC=∠2+∠BDC,
∴∠BOC=∠A+∠1+∠2,
故③正确;
④∠1+∠2+∠3+∠4=180°,
∴∠2+∠3=90°,∠1+∠A=90°,
∴∠1+∠2+∠3+∠4=180°,故此选项正确,
故正确的有4个,
故选:C.
 解:∵BD,CE是△ABC的高,
解:∵BD,CE是△ABC的高,∴∠AEC=90°,∠BDA=90°,
∴∠1+∠A=90°,∠2+∠A=90°,
∴∠1=∠2=90°-∠A,
故①正确;
∵∠ODC=90°,
∴∠3+∠2=90°,
∴∠3=90°-∠2,
∵∠2=90°-∠A,
∴∠A=90°-∠2,
∴∠3=∠A=90°-∠1,
故②正确;
∵∠BDC=∠A+∠1,∠BOC=∠2+∠BDC,
∴∠BOC=∠A+∠1+∠2,
故③正确;
④∠1+∠2+∠3+∠4=180°,
∴∠2+∠3=90°,∠1+∠A=90°,
∴∠1+∠2+∠3+∠4=180°,故此选项正确,
故正确的有4个,
故选:C.
点评:此题主要考查了三角形内角和定理以及三角形外角的性质,灵活利用此性质是解题关键.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
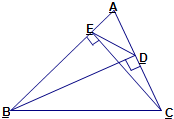 22、如图,已知BD、CE都是△ABC的高,
22、如图,已知BD、CE都是△ABC的高,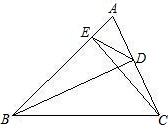 如图,已知BD、CE都是△ABC的高.
如图,已知BD、CE都是△ABC的高.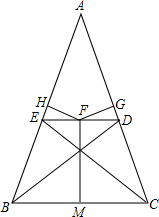 如图,已知BD,CE为△ABC的角平分线,F为DE的中点,点F到AC,AB,BC的距离分别为FG=a,FH=b.FM=c,若c2-c-2ab+
如图,已知BD,CE为△ABC的角平分线,F为DE的中点,点F到AC,AB,BC的距离分别为FG=a,FH=b.FM=c,若c2-c-2ab+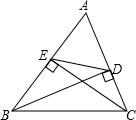 如图,已知BD、CE都是△ABC的高,CE交BD于O,
如图,已知BD、CE都是△ABC的高,CE交BD于O,