��Ŀ����
����Ŀ����ͼ��������ABCD�У�AB=4��P��CD���ϵĶ��㣨P�㲻��C��D�غϣ�������P��ֱ����BC���ӳ��߽��ڵ�E����AD���ڵ�F����CP=CE������DE��BP��BF����CP�Tx����PBF�����ΪS1 �� ��PDE�����ΪS2 �� 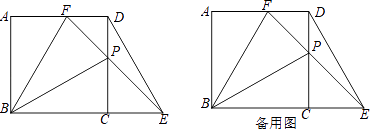
��1����֤��BP��DE��
��2����S1��S2����x�ĺ�������ʽ����д��x��ȡֵ��Χ��
��3���ֱ���PBF=30��͡�PBF=45��ʱ��S1��S2��ֵ��
���𰸡�
��1���⣺��ͼ1�У��ӳ�BP��DE��M��
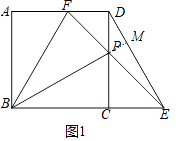
���ı���ABCD�������Σ�
��CB=CD����BCP=��DCE=90�㣬
��CP=CE��
���BCP�ա�DCE��
���BCP=��CDE��
�ߡ�CBP+��CPB=90�㣬��CPB=��DPM��
���CDE+��DPM=90�㣬
���DMP=90�㣬
��BP��DE��
��2���⣺������S1��S2= ![]() ��4+x��x��
��4+x��x�� ![]() ��4��x��x=x2��0��x��4����
��4��x��x=x2��0��x��4����
��3���⣺����ͼ2�У�����PBF=30��ʱ��
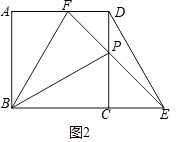
�ߡ�CPE=��CEP=��DPF=45�㣬��FDP=90�㣬
���PFD=��DPF=45�㣬
��DF=DP����AD=CD��
��AF=PC����AB=BC����A=��BCP=90�㣬
���BAF�ա�BCP��
���ABF=��CBP=30�㣬
��x=PC=BCtan30��= ![]() ��
��
��S1��S2=x2= ![]() ��
��
����ͼ3�У�����PBF=45��ʱ����CB�Ͻ�ȡCN=CP������PN��
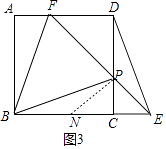
�ɢٿ�֪��ABF�ա�BCP��
���ABF=��CBP��
�ߡ�PBF=45�㣬
���CBP=22.5�㣬
�ߡ�CNP=��NBP+��NPB=45�㣬
���NBP=��NPB=22.5�㣬
��BN=PN= ![]() x��
x��
�� ![]() x+x=4��
x+x=4��
��x=4 ![]() ��4��
��4��
��S1��S2=��4 ![]() ��4��2=48��32
��4��2=48��32 ![]() ��
��
����������1�������ӳ�BP��DE��M��Ȼ������SAS��֤����BCP�ա�DCE������ȫ�������ε����ʿɵõ���BCP=��CDE���ɡ�CBP+��CPB=90�㣬��CPB=��DPM�������Ƴ���CDE+��DPM=90�㣻
��2����������ɵõ�S1-S2=S��PBE-S��PDE��Ȼ�����������ε������ʽ�г�������ϵʽ���ɣ�
��3���ֵ���PBF=30��͡�PBF=45���������ηֱ����PC�ij�����������ã�2���н��۽��м��㼴��.
�����㾫����ͨ��������������ε����ʣ������������ĸ��Ƕ���ֱ�ǣ������߶���ȣ������ε������Խ�����ȣ����һ��ഹֱƽ�֣�ÿ���Խ���ƽ��һ��Խǣ������ε�һ���Խ��߰������ηֳ�����ȫ�ȵĵ���ֱ�������Σ������εĶԽ�����ߵļн���45o�������ε������Խ��߰���������ηֳ��ĸ�ȫ�ȵĵ���ֱ�������μ����Խ����⣮

 �Ǽ�����������ϵ�д�
�Ǽ�����������ϵ�д� â���̸������Ծ�ϵ�д�
â���̸������Ծ�ϵ�д�