题目内容
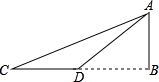 如图,为了测量河对岸的旗杆AB的高度,在点C处测得旗杆顶端A的仰角为30°,沿CB方向前进6米到达D处,在D处测得旗杆顶端A的仰角为45°,则旗杆AB的高度是
如图,为了测量河对岸的旗杆AB的高度,在点C处测得旗杆顶端A的仰角为30°,沿CB方向前进6米到达D处,在D处测得旗杆顶端A的仰角为45°,则旗杆AB的高度是| 3 |
分析:利用AB表示出BC,BD.让BC减去BD等于6,即可求得AB长.
解答:解:设AB=x.
∵tan∠ACB=
,
∴BC=AB÷tan∠ACB=
x,BD=AB÷tan∠ADB=x.
∴CD=BC-BD=(
-1)x=6.
解可得:x=
≈8.2米.
故答案为:8.2,
∵tan∠ACB=
| AB |
| BC |
∴BC=AB÷tan∠ACB=
| 3 |
∴CD=BC-BD=(
| 3 |
解可得:x=
6(
| ||
| 2 |
故答案为:8.2,
点评:本题考查了解直角三角形的应用中的仰角俯角问题,要求学生能借助仰角构造直角三角形并解直角三角形.

练习册系列答案
相关题目
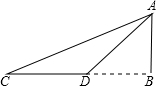 如图,为了测量河对岸某建筑物AB的高度,在平地上点C处测得建筑物顶端A的仰角为30°,沿CB方向前进12米到达D处,在D处测得建筑物顶端A的仰角为45°,求建筑物AB的高度(结果保留根号).
如图,为了测量河对岸某建筑物AB的高度,在平地上点C处测得建筑物顶端A的仰角为30°,沿CB方向前进12米到达D处,在D处测得建筑物顶端A的仰角为45°,求建筑物AB的高度(结果保留根号).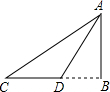 如图,为了测量河对岸的旗杆AB的高度,在点C处测得旗杆顶端A的仰角为30°,沿CB方向前进5米到达D处,在D处测得旗杆顶端A的仰角为45°,则旗杆AB的高度是
如图,为了测量河对岸的旗杆AB的高度,在点C处测得旗杆顶端A的仰角为30°,沿CB方向前进5米到达D处,在D处测得旗杆顶端A的仰角为45°,则旗杆AB的高度是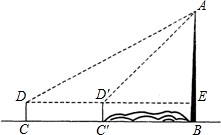 如图,为了测量河对岸的电视塔AB的高度,在D处用测角仪溅得点A的仰角为30°,前进80米,在D′处测得点A的仰角为45°,已知测角仪CD=C′D′=1.2米,求电视塔AB的高度(
如图,为了测量河对岸的电视塔AB的高度,在D处用测角仪溅得点A的仰角为30°,前进80米,在D′处测得点A的仰角为45°,已知测角仪CD=C′D′=1.2米,求电视塔AB的高度( 如图:为了测量河对岸旗杆AB的高度,在点C处测得顶端A的仰角为30°,沿CB方向前进20m达到D处,在D点测得旗杆顶端A的仰角为45°,则旗杆AB的高度为
如图:为了测量河对岸旗杆AB的高度,在点C处测得顶端A的仰角为30°,沿CB方向前进20m达到D处,在D点测得旗杆顶端A的仰角为45°,则旗杆AB的高度为