题目内容
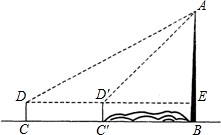 如图,为了测量河对岸的电视塔AB的高度,在D处用测角仪溅得点A的仰角为30°,前进80米,在D′处测得点A的仰角为45°,已知测角仪CD=C′D′=1.2米,求电视塔AB的高度(
如图,为了测量河对岸的电视塔AB的高度,在D处用测角仪溅得点A的仰角为30°,前进80米,在D′处测得点A的仰角为45°,已知测角仪CD=C′D′=1.2米,求电视塔AB的高度(| 3 |
分析:将题目中所涉及到的仰俯角转换为直角三角形内的角,利用解直角三角形的知识求得线段AB的长即可.
解答:解:设AE=x米.
在Rt△AD′E中:∠AD′E=45°,AE=x,
∴D′E=AE=x,
在Rt△ADE中:∠ADE=30°,AE=x,ADE=x+80,
∴由tan30°=
,
得:
=
,
∴x=40
+40,
∴AB=40
+40+1.2≈110米.
答:电视塔AB的高度是110米.
在Rt△AD′E中:∠AD′E=45°,AE=x,
∴D′E=AE=x,
在Rt△ADE中:∠ADE=30°,AE=x,ADE=x+80,
∴由tan30°=
| AE |
| DE |
得:
| x |
| x+80 |
| ||
| 3 |
∴x=40
| 3 |
∴AB=40
| 3 |
答:电视塔AB的高度是110米.
点评:本题考查了仰俯角问题,解决此类问题的关键是正确的将仰俯角转化为直角三角形的内角并选择正确的边角关系解直角三角形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
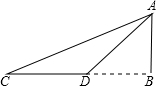 如图,为了测量河对岸某建筑物AB的高度,在平地上点C处测得建筑物顶端A的仰角为30°,沿CB方向前进12米到达D处,在D处测得建筑物顶端A的仰角为45°,求建筑物AB的高度(结果保留根号).
如图,为了测量河对岸某建筑物AB的高度,在平地上点C处测得建筑物顶端A的仰角为30°,沿CB方向前进12米到达D处,在D处测得建筑物顶端A的仰角为45°,求建筑物AB的高度(结果保留根号).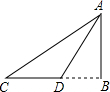 如图,为了测量河对岸的旗杆AB的高度,在点C处测得旗杆顶端A的仰角为30°,沿CB方向前进5米到达D处,在D处测得旗杆顶端A的仰角为45°,则旗杆AB的高度是
如图,为了测量河对岸的旗杆AB的高度,在点C处测得旗杆顶端A的仰角为30°,沿CB方向前进5米到达D处,在D处测得旗杆顶端A的仰角为45°,则旗杆AB的高度是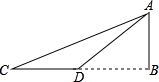 如图,为了测量河对岸的旗杆AB的高度,在点C处测得旗杆顶端A的仰角为30°,沿CB方向前进6米到达D处,在D处测得旗杆顶端A的仰角为45°,则旗杆AB的高度是
如图,为了测量河对岸的旗杆AB的高度,在点C处测得旗杆顶端A的仰角为30°,沿CB方向前进6米到达D处,在D处测得旗杆顶端A的仰角为45°,则旗杆AB的高度是 如图:为了测量河对岸旗杆AB的高度,在点C处测得顶端A的仰角为30°,沿CB方向前进20m达到D处,在D点测得旗杆顶端A的仰角为45°,则旗杆AB的高度为
如图:为了测量河对岸旗杆AB的高度,在点C处测得顶端A的仰角为30°,沿CB方向前进20m达到D处,在D点测得旗杆顶端A的仰角为45°,则旗杆AB的高度为