题目内容
【题目】如图,矩形纸片ABCD中,点E是AD的中点,且AE=1,BE的垂直平分线MN恰好过点C.则矩形的一边AB的长度为( ) 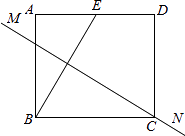
A.1
B.![]()
C.![]()
D.2
【答案】C
【解析】解:如图,连接EC. 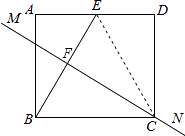
∵FC垂直平分BE,
∴BC=EC(线段垂直平分线的性质)
又∵点E是AD的中点,AE=1,AD=BC,
故EC=2,
利用勾股定理可得AB=CD= ![]() =
= ![]() .
.
故选:C.
【考点精析】根据题目的已知条件,利用线段垂直平分线的性质和勾股定理的概念的相关知识可以得到问题的答案,需要掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.

练习册系列答案
相关题目
【题目】青少年“心理健康“问题越来越引起社会的关注,某中学为了了解学校600名学生的心理健康状况,举行了一次“心理健康“知识测试.并随机抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本,绘制了下面未完成的频数分布表和频数分布直方图(如图).请回答下列问题:
分组 | 频数 | 频率 |
50.5~60.5 | 4 | 0.08 |
60.5~70.5 | 14 | 0.28 |
70.5~80.5 | 16 | |
80.5~90.5 | ||
90.5~100.5 | 10 | 0.20 |
合计 | 1.00 |

(1)填写频数分布表中的空格,并补全频数分布直方图;
(2)若成绩在70分以上(不含70分)为心理健康状况良好.若心理健康状况良好的人数占总人数的70%以上,就表示该校学生的心理健康状况正常,否则就需要加强心理辅导.请根据上述数据分析该校学生是否需要加强心理辅导,并说明理由.