题目内容
图中正方形GFCD和正方形AEHG的边长都是整数,它们的面积之和是117,P是AE上一点,Q是CD上一点.则三角形BCH的面积是 ;四边形PHQG的面积是 .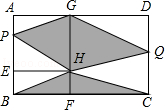

22.5 45
试题分析:先设正方形GFCD的边长为x,正方形AEHG的边长为y(且x<y,x、y都是正整数),再根据两个正方形的面积和求出两个正方形的边长,再由正方形及三角形的面积公式即可求解.
解:设正方形GFCD的边长为x,正方形AEHG的边长为y(且x<y,x、y都是正整数),
则有x2+y2=117,解得x=6,y=9.
所以三角形BCH的面积s1=
 (x+y)(y﹣x)=
(x+y)(y﹣x)= (6+9)×(9﹣6)=
(6+9)×(9﹣6)= ×15×3=22.5.
×15×3=22.5.四边形PHQG的面积S2=
 x2+
x2+ xy=
xy= ×62+
×62+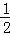 ×6×9=18+27=45.
×6×9=18+27=45.故答案为:22.5,45.
点评:本题考查的是方程的整数根及三角形的面积公式,根据题意列出方程,求出两正方形的边长是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


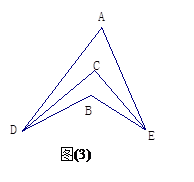
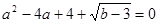 ,则笫三边c的长度是_____.
,则笫三边c的长度是_____.