��Ŀ����
����Ŀ��������������
�ڼ�����������һ�����������ϵذ���![]() ����������ƽ������������Խ��Խ�ӽ�1����1��
����������ƽ������������Խ��Խ�ӽ�1����1��
��������⡿
����һ��ʵ�������ϵؽ��С����Գ���k���ټ��ϳ���b�������㣬��ʲô���ɣ�
���������⡿
���ǿ��ÿ�ͼ��ʾ����������̣���ͼa����
Ҳ����ͼ����������ͼ1����x���ϱ�ʾ��x1������ֱ��y=kx+b��ȷ���㣨x1��y1��������ֱ��y=x��ȷ��������Ϊy1�ĵ㣨x2��y1����Ȼ����x����ȷ����Ӧ����x2�������Դ����ƣ�
��������⡿
�о�����ʵ��x1ʱ�������������n�IJ������ӣ�������x�������仯��
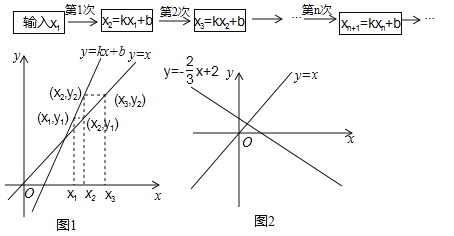
��1����k=2��b=��4���õ�ʲô���ۣ������������������3��4��5���й۲��о���
��2����k��1���ֵõ�ʲô���ۣ���˵�����ɣ�
��3������![]() ��b=2������x���ϱ�ʾ��x1����ͼ2��ʾ��������x���ϱ�ʾx2��x3��x4����д���о����ۣ�
��b=2������x���ϱ�ʾ��x1����ͼ2��ʾ��������x���ϱ�ʾx2��x3��x4����д���о����ۣ�
��������ʵ��x1ʱ��������xn������ȣ���Խ��Խ�ӽ�����m��ֱ��д��k��ȡֵ��Χ��m��ֵ���ú�k��b�Ĵ���ʽ��ʾ��
���𰸡���1����x1��4ʱ�������������n�����ӣ�������xnԽ��ԽС����x1=4ʱ�������������n�����ӣ�������xn��ֵ���ֲ��䣬������4����x1��4ʱ�������������n�����ӣ�������xnԽ��Խ��
����2����x1��![]() ʱ�������������n�����ӣ�xnԽ��Խ������x1��
ʱ�������������n�����ӣ�xnԽ��Խ������x1��![]() ʱ�������������n�����ӣ�xnԽ��ԽС����x1=
ʱ�������������n�����ӣ�xnԽ��ԽС����x1=![]() ʱ�������������n�����ӣ�xn���ֲ�������3��������������������ӣ�������Խ��Խ�ӽ�
ʱ�������������n�����ӣ�xn���ֲ�������3��������������������ӣ�������Խ��Խ�ӽ�![]() ������1��k��1��k��0��m=
������1��k��1��k��0��m=![]() ��
��
��������
�����������1����x1��4��x1=4��x1��4�������ν�ɣ�
��2����x1��![]() ��x1��
��x1��![]() ��x1=
��x1=![]() �������ν�ɣ�
�������ν�ɣ�
��3������ͼ2�У�����ͼ�Σ�����ͼ�ɽ�����⣬xn��ֵԽ��Խ�ӽ���ֱ�߽���ĺ����꣮
�ڸ���ǰ���̽�����ɽ�����⣮
�����������1����k=2��b=��4��y=2x��4��ȡx1=3����x2=2��x3=0��x4=��4����
ȡx1=4����x2x3=x4=4����
ȡx1=5����x2=6��x3=8��x4=12�����ɴ˷��֣�
��x1��4ʱ�������������n�����ӣ�������xnԽ��ԽС��
��x1=4ʱ�������������n�����ӣ�������xn��ֵ���ֲ��䣬������4��
��x1��4ʱ�������������n�����ӣ�������xnԽ��Խ��
��2����x1��![]() ʱ�������������n�����ӣ�xnԽ��Խ��
ʱ�������������n�����ӣ�xnԽ��Խ��
��x1��![]() ʱ�������������n�����ӣ�xnԽ��ԽС��
ʱ�������������n�����ӣ�xnԽ��ԽС��
��x1=![]() ʱ�������������n�����ӣ�xn���ֲ��䣮
ʱ�������������n�����ӣ�xn���ֲ��䣮
���ɣ���ͼ1�У�ֱ��y=kx+b��ֱ��y=x�Ľ�������Ϊ��![]() ��
��![]() ������x1��
������x1��![]() ʱ������ͬһ��x��ֵ��kx+b��x����y1��x1
ʱ������ͬһ��x��ֵ��kx+b��x����y1��x1
��y1=x2����x1��x2��ͬ��x2��x3������xn���൱x1��![]() ʱ�������������n�����ӣ�xnԽ��Խ��
ʱ�������������n�����ӣ�xnԽ��Խ��
ͬ������x1��![]() ʱ�������������n�����ӣ�xnԽ��ԽС��
ʱ�������������n�����ӣ�xnԽ��ԽС��
��x1=![]() ʱ�������������n�����ӣ�xn���ֲ��䣮
ʱ�������������n�����ӣ�xn���ֲ��䣮
��3�����������ϱ�ʾ��x1��x2��x3��ͼ2��ʾ��
����������������ӣ�������Խ��Խ�ӽ�![]() ��
��
���ɣ�2����֪����1��k��1��k��0����![]() ��ȥy�õ�x=
��ȥy�õ�x=![]() �����ɢ�̽����֪��m=
�����ɢ�̽����֪��m=![]() ��
��