Question

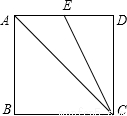
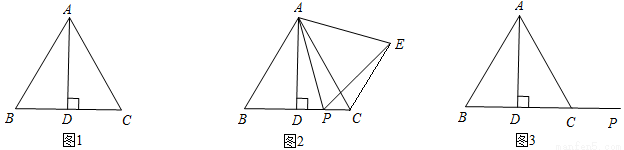
在等边三角形ABC中，AD⊥BC于点D．

（1）如图1，请你直接写出线段AD与BC之间的数量关系: AD= BC　；

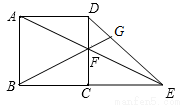
（2）如图2，若P是线段BC上一个动点（点P不与点B、C重合），联结AP，将线段AP绕点A逆时针旋转60°，得到线段AE，联结CE，猜想线段AD、CE、PC之间的数量关系，并证明你的结论；

（3）如图3，若点P是线段BC延长线上一个动点，（2）中的其他条件不变，按照（2）中的作法，请在图3中补全图形，并直接写出线段AD、CE、PC之间的数量关系．

 

 

Answer 1

（1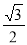）；（2）AD=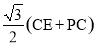，理由见解析；（3）补图见解析，AD=．

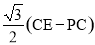【解析】

试题分析：（1）根据等边三角形的性质，得∠B=600，AB=BC，所以根据锐角三角函数定义和特殊角的三角函数值求得AD=．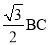

（2）根据等边三角形和旋转的性质，证明△ABP≌△ACE即可求得结论．

（3）类同（2）的证明．

试题解析：（1）∵等边三角形ABC，∴∠B=600，AB=BC．

又∵AD⊥BC，∴．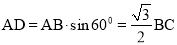

（2）AD=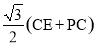．理由如下：

∵线段AP绕点A逆时针旋转60°，得到线段AE，∴∠PAE=60°，AP=AE．

∵等边三角形ABC，∴∠BAC=60°，AB=AC．

∴∠BAC﹣∠PAC=∠PAE﹣∠PAC．∴∠BAP=∠CAE．

在△ABP和△ACE中，∵，

∴△ABP≌△ACE．∴BP=CE．

∵BP+PC=BC，∴CE+ PC=BC．

∵AD=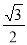BC，∴AD=．

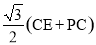（3）补全图形如图：

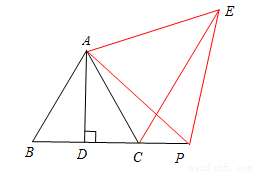
∵线段AP绕点A逆时针旋转60°，得到线段AE，∴∠PAE=60°，AP=AE．

∵等边三角形ABC，∴∠BAC=60°，AB=AC．

∴∠BAC+∠PAC=∠PAE+∠PAC．∴∠BAP=∠CAE．

在△ABP和△ACE中，∵，

∴△ABP≌△ACE．∴BP=CE．

∵，∴．

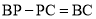∵AD=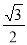BC，∴AD=．

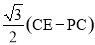考点：1．线动旋转问题；2．等边三角形的性质；3．全等三角形的判定和性质；4．锐角三角函数定义；5．特殊角的三角函数值．