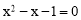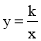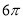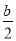Question

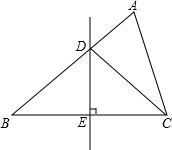
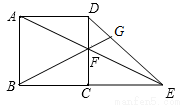
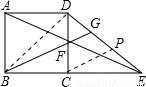
已知正方形ABCD的边长为2，E为BC边的延长线上一点，CE＝2，联结AE，与CD交于点F，联结BF并延长与线段DE交于点G，则BG的长为 ．

 

 

Answer 1

．

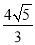【解析】

试题分析：利用全等三角形的判定AAS得出△ADF≌△ECF，进而得出FG是△DCP的中位线，得出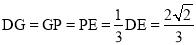，再利用勾股定理得出BG的长即可：

如图，过点C作CP∥BG，交DE于点P．

∵BC=CE=2，∴CP是△BEG的中位线．∴P为EG的中点．

又∵AD=CE=1，AD∥CE，

∴在△ADF和△ECF中，∠AFD＝∠EFC，∠ADC＝∠FCE，AD＝CE，

∴△ADF≌△ECF（AAS）．∴CF=DF．

又CP∥FG，∴FG是△DCP的中位线．∴G为DP的中点．

∵CD=CE=2，∴DE=．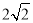

∴．

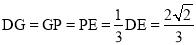连接BD，

易知∠BDC=∠EDC=45°，∴∠BDE=90°．

又∵BD=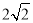

∴．

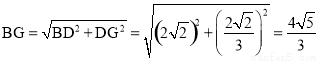考点：1．正方形的性质；2．全等三角形的判定和性质；3．勾股定理；4．三角形中位线定理．