��Ŀ����
����Ŀ��Ϊ�˴���ȫ���������У�ij����Ҫ����һ�����������ڵ����������üס����������ͣ�����������������12�˲�����ɣ���֧���˷ѹ�4 800Ԫ�����ס���������������˶����������ҳ����������Ǽ׳���2������֪�ҳ�ÿ���˷ѱȼ׳���200Ԫ��
(1)�ֱ�����ס�������ÿ�˵��˷ѣ�
(2)���������ü׳�����˶�������������ˣ�
(3)��ͬʱ���üס�����������׳���x�ˣ��ҳ���y�ˣ���������˶�����������x��y��Ϊ��������
�ٵ�x��10ʱ��y�� ����y��10ʱ��x�� ��
���ú�x�Ĵ���ʽ��ʾy��
̽����
(4)��(3)�������£�
���ú�x�Ĵ���ʽ��ʾ���˷�w��
��Ҫ�����˷Ѳ�����4 000Ԫ���׳�������˶����ˣ�
���𰸡���1���ס�������ÿ�˵��˷ѷֱ�Ϊ300Ԫ��100Ԫ����2���������ü׳�����˶�����������18�ˣ���3����16��13��y=36��2x����4����w=100x��3600���ڼ׳��������4�ˣ�
��������
��1����ס�������ÿ�˵��˷ѷֱ�ΪmԪ��nԪ�����������г���Ԫһ�η����飬��⼴�ɣ�
��2���赥�����ü׳�����˶�����������![]() �ˣ��������۳���ʽ���̣���⼴�ɣ�
�ˣ��������۳���ʽ���̣���⼴�ɣ�
��3�����г���ʽ������⼴�ɣ�
�ڸ������⣬�г���ʽ����ת����ʽ���ɣ�
��4���ٽ�ϣ�1���ͣ�3���Ľ��ۣ��г�������ϵʽ���ɣ�
�ڸ��������г�����ʽ����⼴��.
(1)��ס�������ÿ�˵��˷ѷֱ�ΪmԪ��nԪ�������⣬��
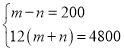 ���
���![]()
�𣺼ס�������ÿ�˵��˷ѷֱ�Ϊ300Ԫ��100Ԫ��
(2)�赥�����ü׳�����˶�����������![]() �ˣ������⣬��
�ˣ������⣬��
![]() ���
���![]()
�����飬![]() ��ԭ���̵Ľ⣬�ҷ������⣮
��ԭ���̵Ľ⣬�ҷ������⣮
�𣺵������ü׳�����˶�����������18�ˣ�
(3)�������⣬��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
�������⣬��![]() ��
��
��y=36��2x��
(4)���ɣ�1���ͣ�3���������˷�Ϊw=300x��100y=300x��100(36��2x) =100x��3600��
�������⣬��100x��3600��4 000��
��x��4��
�𣺼׳��������4�ˣ�

 �п�������㾫��ϵ�д�
�п�������㾫��ϵ�д� ������ĩ��ϰ��ѵ��ϵ�д�
������ĩ��ϰ��ѵ��ϵ�д�