ЬтФПФкШн
ЁОЬтФПЁПЮвЙњБпЗРОжНгЕНЧщБЈЃЌНќКЃДІгавЛПЩвЩДЌжЛ![]() е§ЯђЙЋКЃЗНЯђКНааЃЌБпЗРВПбИЫйХЩГіПьЭЇ
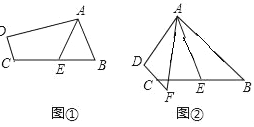
е§ЯђЙЋКЃЗНЯђКНааЃЌБпЗРВПбИЫйХЩГіПьЭЇ![]() зЗИЯШчЭМ1ЃЌЭМ2жа
зЗИЯШчЭМ1ЃЌЭМ2жа![]() ЗжБ№БэЪОСНДЌЯрЖдКЃАЖЕФОрРы
ЗжБ№БэЪОСНДЌЯрЖдКЃАЖЕФОрРы![]() (КЃРя)гызЗИЯЪБМф
(КЃРя)гызЗИЯЪБМф![]() (Зж)жЎМфЕФЙиЯЕ.
(Зж)жЎМфЕФЙиЯЕ.

ИљОнЭМЯѓЛиД№ЮЪЬтЃК
(1)ФФЬѕЯпБэЪО![]() ЕНКЃАЖЕФОрРыгызЗИЯЪБМфжЎМфЕФЙиЯЕЃП
ЕНКЃАЖЕФОрРыгызЗИЯЪБМфжЎМфЕФЙиЯЕЃП
(2)![]() ФФИіЫйЖШПьЃП
ФФИіЫйЖШПьЃП
(3)15ЗжжгФк![]() ФмЗёзЗЩЯ
ФмЗёзЗЩЯ![]() ЃПЮЊЪВУДЃП
ЃПЮЊЪВУДЃП
(4)ШчЙћвЛжБзЗЯТШЅЃЌФЧУД![]() ФмЗёзЗЩЯ
ФмЗёзЗЩЯ![]() ЃП
ЃП
(5)ЕБ![]() ЬгРыКЃАЖ12КЃРяЪБЃЌ
ЬгРыКЃАЖ12КЃРяЪБЃЌ![]() НЋЮоЗЈЖдЦфНјааМьВщЃЌееДЫЫйЖШЃЌ
НЋЮоЗЈЖдЦфНјааМьВщЃЌееДЫЫйЖШЃЌ![]() ФмЗёдк
ФмЗёдк![]() ЬгШыЙЋКЃЧАНЋЦфРЙНиЃПЮЊЪВУДЃП
ЬгШыЙЋКЃЧАНЋЦфРЙНиЃПЮЊЪВУДЃП
(6)![]() гы
гы![]() ЖдгІЕФСНИівЛДЮКЏЪ§
ЖдгІЕФСНИівЛДЮКЏЪ§![]() гы
гы![]() жаЃЌ
жаЃЌ![]() ЕФЪЕМЪвтвхИїЪЧЪВУДЃППЩвЩДЌжЛ
ЕФЪЕМЪвтвхИїЪЧЪВУДЃППЩвЩДЌжЛ![]() гыПьЭЇ
гыПьЭЇ![]() ЕФЫйЖШИїЪЧЖрЩйЃП
ЕФЫйЖШИїЪЧЖрЩйЃП
ЁОД№АИЁП(1)l1БэЪОBЃЛ(2)BЕФЫйЖШПьЃЛ(3)15ЗжжгВЛФмзЗЩЯAЃЛ(4)BвЛЖЈФмзЗЩЯAЃЛ(5)BФмдкAЬгШыЙЋКЃЧАзЗЩЯЃЛ(6)МћНтЮі.
ЁОНтЮіЁП
(1)BзЗИЯAЃЌЫљвдBЕНКЃАЖЕФОрРыИќНќЃЛ
(2)жБЯпЧуаБдНРїКІЫЕУїЃЌБфЛЏдНПьЃЌвВОЭЪЧЫйЖШПьЃЛ
(3)РћгУД§ЖЈЯЕЪ§ЗЈЧѓГіКЏЪ§НтЮіЪНЃЌДњШыt=15ЃЌЧѓГіsжЕМДПЩЕУГіЃЛ
(4)ИљОнСНДЌЕФЫйЖШПьТ§НјааЗжЮіМДПЩЃЛ
(5)ДњШыs=12ЧѓГіtжЕНјааБШНЯЃЌОЭПЩвдХаЖЯГіBФмЗёдкAНјШыЙЋКЃЧАНЋЦфРЙНиЃЛ
(6)ИљОнЬтвтПЩжЊ![]() БэЪОПЩвЩДЌжЛAгыПьЭЇBЕФЫйЖШЃЌИљОн(3)жаЕФНтЮіЪНМДПЩЕУ.
БэЪОПЩвЩДЌжЛAгыПьЭЇBЕФЫйЖШЃЌИљОн(3)жаЕФНтЮіЪНМДПЩЕУ.
(1)ЁпМЦЪБПЊЪМBДгКЃЗРОжГіЗЂ
Ёрl1БэЪОBЃЛ
(2)Ёпl1БШl2ИќЖИЃЌ
ЁрBЕФЫйЖШПьЃЛ
(3)ЩшBгыAЕФНтЮіЪНЗжБ№ЮЊs1=k1tКЭs2=k2t+bИљОнЭМЯѓЕУ
10k1=5ЃЌНтЕУk1=![]() ЃЌ
ЃЌ
![]() ЃЌНтЕУ
ЃЌНтЕУ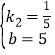 ЃЌ
ЃЌ
Ёрs1ЃН![]() tЃЌs2ЃН
tЃЌs2ЃН![]() t+5ЃЌ
t+5ЃЌ
ЕБt=15ЪБЃЌ![]() ЁС15ЃН7.5ЃЌ
ЁС15ЃН7.5ЃЌ![]() ЁС15+5ЃН8ЃЌ
ЁС15+5ЃН8ЃЌ
7.5ЃМ8ЃЌ
Ыљвд15ЗжжгВЛФмзЗЩЯAЃЛ
(4)BвЛЖЈФмзЗЩЯAЃЛ
(5)ЕБs=12ЪБЃЌ12=![]() tЃЌНтЕУЃКt=24ЃЌ
tЃЌНтЕУЃКt=24ЃЌ
12=![]() t+5ЃЌНтЕУЃКt=35ЃЌ
t+5ЃЌНтЕУЃКt=35ЃЌ
24ЃМ35ЃЌ
ЫЕУїОрРыКЃАЖ12КЃРяAгУЕФЪБМфЖрЃЌ
ЁрBФмдкAЬгШыЙЋКЃЧАзЗЩЯЃЛ
(6)k1БэЪОПьЭЇBЕФЫйЖШЃЌk2БэЪОПЩвЩДЌжЛAЕФЫйЖШЃЌ
гЩ(3)ЕФНтЮіЪНПЩжЊПЩвЩДЌжЛAЕФЫйЖШЪЧ![]() КЃРя/ЗжЃЌПьЭЇBЕФЫйЖШЪЧ
КЃРя/ЗжЃЌПьЭЇBЕФЫйЖШЪЧ![]() КЃРя/Зж.
КЃРя/Зж.

 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ