题目内容
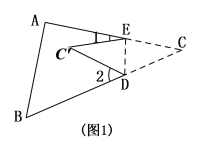
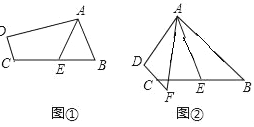
【题目】（1）如图①，在四边形ABCD中，AB∥DC，E是BC的中点，若AE是∠BAD的平分线，求证：AD=DC+AB，
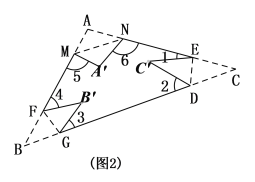
（2）如图②，在四边形ABCD中，AB∥DC，F是DC延长线上一点，连接AF，E是BC的中点，若AE是∠BAF的平分线，求证：AB=AF+CF.
【答案】（1）证明见解析； （2）证明见解析.
【解析】
（1）延长AE交DC的延长线于点F，证明△AEB≌△FEC，根据全等三角形的性质得到AB=FC，根据等腰三角形的判定得到DF=AD，证明结论；
（2）延长AE交DF的延长线于点G，利用同（1）相同的方法证明.
解：（1）延长AE交DC的延长线于点F，
∵E是BC的中点，
∴CE=BE，
∵AB∥DC，
∴∠BAE=∠F，
在△AEB和△FEC中，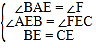
，
∴△AEB≌△FEC，
∴AB=FC，
∵AE是∠BAD的平分线，
∴∠BAE=∠EAD，
∵AB∥CD，
∴∠BAE=∠F，
∴∠EAD=∠F，
∴AD=DF，
∴AD=DF=DC+CF=DC+AB，
（2）如图②，延长AE交DF的延长线于点G，
∵E是BC的中点，
∴CE=BE，
∵AB∥DC，
∴∠BAE=∠G，
在△AEB和△GEC中， 
，
∴△AEB≌△GEC，
∴AB=GC，
∵AE是∠BAF的平分线，
∴∠BAG=∠FAG，
∵AB∥CD，
∴∠BAG=∠G，
∴∠FAG=∠G，
∴FA=FG，
∴AB=CG=AF+CF.
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
