题目内容
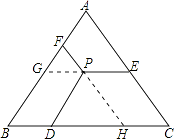
【题目】如图，△ABC是等边三角形，点P是三角形内的任意一点，PD∥AB，PE∥BC，PF∥AC，若△ABC的周长为36，则PD+PE+PF=（ ）
A.12
B.8
C.4
D.3
【答案】A
【解析】解：如图，延长EP、FP分别交AB、BC于G、H，则由PD∥AB，PE∥BC，PF∥AC，
∴四边形PGBD和四边形EPHC是平行四边形，
∴PG=BD，PE=HC，
又△ABC是等边三角形，
又有PF∥AC，PD∥AB可得△PFG，△PDH是等边三角形，
∴PF=PG=BD，PD=DH，
又△ABC的周长为36，
∴PD+PE+PF=DH+HC+BD=BC= 
×36=12，
故A符合题意.
故答案为：A．
延长EP、FP分别交AB、BC于G、H，易证得四边形PGBD、四边形EPHC是平行四边形以及△PFG、△PDH是等边三角形，进而根据三角形的周长可求得.
练习册系列答案
小学夺冠AB卷系列答案
相关题目
