��Ŀ����
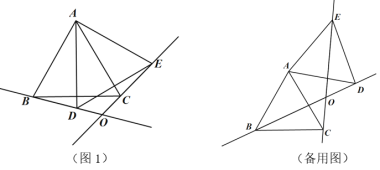
����Ŀ����֪��ABC�DZ߳�Ϊ6�ĵȱ������Σ�����ABC�Ƶ�A��ʱ����ת������0��![]() ��
��![]() 180�����õ���ADE��BD��EC����ֱ���ཻ�ڵ�O��
180�����õ���ADE��BD��EC����ֱ���ཻ�ڵ�O��
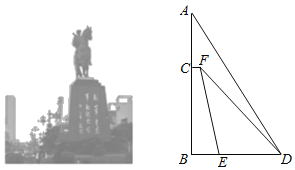
��1����ͼ1����0��![]() ��
��![]() 60��ʱ����BOC�Ķ����Ƿ�仯�������䣬�����BOC�Ķ��������仯��ֱ��д����BOC�Ķ����ı仯��Χ��
60��ʱ����BOC�Ķ����Ƿ�仯�������䣬�����BOC�Ķ��������仯��ֱ��д����BOC�Ķ����ı仯��Χ��
��2������ת�����У�����BDE��ֱ��������ʱ����BD�ij���
��3��������60����120������ת�����У�ֱ��д����O�˶���·������
���𰸡���1�����䣬![]() ��2��
��2��![]() ����3��
����3��![]()
��������
��1����֤����ABD�ա�ACE��Ȼ����ݽǵĴ����ɵó���BOC=120����
��2�����Ƴ���BDA=30��������AB=AD=6���ó���ABD=30������AM��BD��M���ڡ�ABM�У���ABM=30����AB=6����BMA=90�������ɵó���
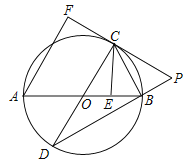
��3����ͼ��AD��AE��J�����ABC�����Բ��Բ��ΪK��֤����AOC��120�����Ƴ���O���˶��켣��KΪԲ�ģ�KC�뾶��Բ����Բ�Ľ�Ϊ60�������ɵó��𰸣�
�⣺��1����AD=AE��AB=AC����BAD+��DAC=��DAC+��CAE=60����
���BAD=��CAE��
���ABD�ա�ACE��
���AEC=��ADB��
�ߡ�ADO+��ADB=180����
���ADO+��AEC=180����
���DAE+��BOC=180����
�ߡ�DAE=60����
���BOC=120����
���BOC�Ķ������䣬��BOC=120����
��2���ߡ�BDE��ֱ�������Σ�
���BDE=90����
�ߡ�BDA+��ADE=90������ADE=60����
���BDA=30����
��AB=AD=6��
���ABD=30����
��AM��BD��M��
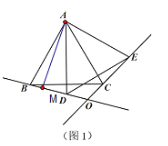
�ڡ�ABM�У���ABM=30����AB=6����BMA=90����
��BM=![]() ��
��
��BD=6![]() ��
��
��3����ͼ�У�AD��AE��J�����ABC�����Բ��Բ��ΪK��
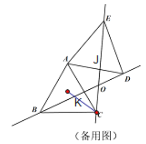
�ߡ�ABD�ա�ACE��
���ODJ����AEJ��
�ߡ�AJE����OJD��
���EAJ����JOD��60����
���AOC��120����
���O���˶��켣��KΪԲ�ģ�KC�뾶��Բ����Բ�Ľ�Ϊ60����
�൱����60����120������ת�����У�KC=![]() ��
��![]() =
=![]() ��
��
![]() =
=![]() ��
��

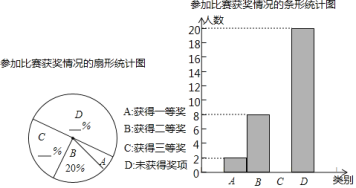
 �ο�����������100��ϵ�д�
�ο�����������100��ϵ�д� �Űٷֿ�ʱ����ϵ�д�
�Űٷֿ�ʱ����ϵ�д�����Ŀ��Ϊ�˽�ѧ��������������֪ʶ���������ǿѧ��������ʶ��ijѧУ����������������������������֪ʶ���Ի���ִӸ�У�ߡ����꼶�и������ȡ20��ѧ���IJ��Գɼ�������10�֣�6�ּ�6������Ϊ�ϸ��������������ͷ�������������˲�����Ϣ��
���꼶20��ѧ���IJ��Գɼ�Ϊ��
7��8��7��9��7��6��5��9��10��9��8��5��8��7��6��7��9��7��10��6��
�ߡ����꼶��ȡ��ѧ���IJ��Գɼ���ƽ��������������λ����8�ּ�����������ռ�ٷֱ����±���ʾ��
�꼶 | ƽ���� | ���� | ��λ�� | 8�ּ�����������ռ�ٷֱ� |
���꼶 | 7.5 | a | 7 | 45% |
���꼶 | 7.5 | 8 | b | c |
���꼶20��ѧ���IJ��Գɼ�����ͳ��ͼ��ͼ��
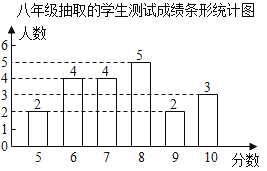
����������Ϣ������������⣺
��1��ֱ��д���������е�a��b��c��ֵ��
��2�������������ݣ�����Ϊ��У�ߡ����꼶���ĸ��꼶ѧ��������������֪ʶ�Ϻã���˵�����ɣ�д��һ�����ɼ��ɣ���
��3����У�ߡ����꼶��1200��ѧ���μ��˴˴β��Ի�����ƲμӴ˴β��Ի�ɼ��ϸ��ѧ�������Ƕ��٣�