题目内容
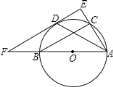
【题目】如图,![]() 是
是![]() 的外接圆,
的外接圆,![]() 的平分线与
的平分线与![]() 相交于点
相交于点![]() ,过点
,过点![]() 作
作![]() 的切线
的切线![]() ,与
,与![]() 的延长线交于点
的延长线交于点![]() ,与
,与![]() 的延长线交于点
的延长线交于点![]() .
.
![]() 试判断
试判断![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
![]() 若
若![]() ,
,![]() ,求
,求![]() 的半径.
的半径.
【答案】(1)BC∥EF,理由见解析;(2)⊙O的半径为2.5.
【解析】
(1)连接OD,根据切线证明AE∥OD,∠E=90°,在根据直径所对圆周角是直角得∠ACB=90°,即可证明;(2)根据切线定理即可解题.
(1)BC∥EF,理由如下:
连结OD.
∵EF是⊙O的切线交⊙O于点D,
∴OD⊥EF,∠ODA=∠OAD.
∴∠ODF=90°.
∵AD平分∠BAC,
∴∠BAD=∠EAD,
∴∠ODA=∠EAD,
∴OD∥AE,
∴∠ODF=∠E=90°.
∵AB是⊙O的直径,
∴∠ACB=90°
∴∠ACB=∠E,
∴BC∥EF;
(2)∵EF是⊙O的切线,
∴DF2=BFAF.
∵FD=6,AF=9,
∴36=9BF,
∴BF=4,
∴AB=5,
∴OB=2.5
答:⊙O的半径为2.5.

练习册系列答案
相关题目