题目内容
小赵投资销售一种进价为每件20元的护眼台灯.销售过程中发现,当月内销售单价不变,则月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数: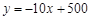 .
.
(1)设小赵每月获得利润为w(元),当销售单价定为多少元时,每月可获得最大利润?并求出最大利润.
(2)如果小赵想要每月获得的利润不低于2000元,那么如何制定销售单价才可以实现这一目标?
(1)当销售单价定为35元时,每月获得的利润最大,最大利润为2250元;
(2)如果小赵想要每月获得的利润不低于2000元,那么他的销售单价应不低于30元而不高于40元.
解析试题分析:(1)根据每月利润=单件利润×每月销量,从而得出w与x的关系式,利用配方法求最值即可;
(2)由题意得,w≥2000,解不等式即可得出答案.
试题解析:(1)由题意,得:w=(x﹣20)•y=(x﹣20)•(﹣10x+500)
=﹣10x2+700x﹣10000
=﹣10(x﹣35)2+2250,
当x=35时,w取得最大,最大利润为2250元.
答:当销售单价定为35元时,每月获得的利润最大,最大利润为2250元.
(2)由题意得:﹣10x2+700x﹣10000≥2000,
解得:30≤x≤40.
答:如果小赵想要每月获得的利润不低于2000元,那么他的销售单价应不低于30元而不高于40元.
考点:二次函数的应用.

某批发商以每件50元的价格购进800件T恤,第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一次性清仓销售,清仓时单价为40元,设第二个月单价降低x元.
(1)填表:(不需化简)
| 时间 | 第一个月 | 第二个月 | 清仓时 |
| 单价(元) | 80 | | 40 |
| 销售量(件) | 200 | | |


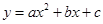 过A、B、C三点,AB=10,tan∠CAD=
过A、B、C三点,AB=10,tan∠CAD= .
. ,0),如图所示:抛物线
,0),如图所示:抛物线 经过点B。
经过点B。
