题目内容
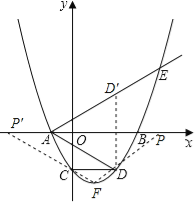
【题目】如图,二次函数y=a(x2-2mx-3m2)(其中a,m为常数,且a>0,m>0)的图象与x轴分别交于点A、B(点A位于点B左侧),与y轴交于点C(0,-3),点D在二次函数图象上,且CD∥AB,连AD;过点A作射线AE交二次函数于点E,使AB平分∠DAE.
(1)当a=1时,求点D的坐标;
(2)证明:无论a、m取何值,点E在同一直线上运动;
(3)设该二次函数图象顶点为F,试探究:在x轴上是否存在点P,使以PF、AD、AE为边构成的三角形是以AE为斜边的直角三角形?如果存在,请用含m的代数式表示点P的横坐标,如果不存在,请说明理由.

【答案】(1)D(2,-3);(2)证明见解析;(3)P(-3m,0)或(5m,0).
【解析】试题分析:(1)根据题意将a=1,C(0,﹣3)代入y=a(x2﹣2mx﹣3m2),进而求出m的值,即可得出答案;
(2)首先根据题意表示出A,B,C,D,进而联立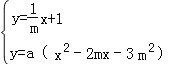 ,求出E点坐标即可得出答案;
,求出E点坐标即可得出答案;
(3)由(2)得:F(m,﹣4)、E(4m,5)、A(﹣m,0)、D(2m,﹣3),再利用PF,AD,AE的关系得出答案.
解:(1)当a=1时,y=a(x2﹣2mx﹣3m2)=x2﹣2mx﹣3m2,
∵与y轴交于点C(0,﹣3),
∴﹣3m2=﹣3,
解得:m=±1,
∵m>0,
∴m=1,
∴抛物线解析式为:y=x2﹣2x﹣3=(x﹣1)2+4,
故抛物线顶点坐标为:D(2,﹣3);
(2)作D关于AB对称的点D′必在AE上,
当y=0,则0=a(x2﹣2mx﹣3m2),
解得:x1=﹣m,x2=3m,
当x=0,y=﹣3am2,
可得:A(﹣m,0)、B(3m,0),C(0,﹣3am2),D(2m,﹣3am2)
∴D′(2m,3am2),
∵抛物线过点C,
∴﹣3am2=﹣3,
则am2=1,
∴直线AD′的解析式为:y=![]() x+1,
x+1,
联立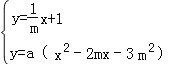 ,整理得x2﹣3mx﹣4m2=0
,整理得x2﹣3mx﹣4m2=0
解得x1=4m,x2=﹣m(舍去)
∴E(4m,5)
∴E在y=5上运动;
(3)由(2)得:F(m,﹣4)、E(4m,5)、A(﹣m,0)、D(2m,﹣3)
设P(b,0)
∴PF2=(m﹣b)2+16,AD2=9m2+9,AE2=25m2+25
∴(m﹣b)2+16+9m2+9=25m2+25,
解得:b1=﹣3m,b2=5m
∴P(﹣3m,0)或(5m,0).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
