题目内容
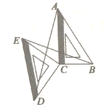
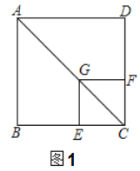
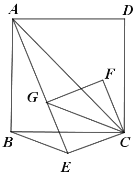
【题目】如图(1),已知点![]() 在正方形
在正方形![]() 的对角线
的对角线![]() 上,
上,![]() 垂足为点
垂足为点![]() ,垂足为点
,垂足为点![]() .
.
(1)证明与推断:
![]() 求证:四边形
求证:四边形![]() 是正方形;
是正方形;
![]() 推断:
推断:![]() 的值为_ _;
的值为_ _;
(2)探究与证明:
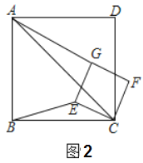
将正方形![]() 绕点
绕点![]() 顺时针方向旋转
顺时针方向旋转![]() 角
角![]() ,如图(2)所示,试探究线段
,如图(2)所示,试探究线段![]() 与
与![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
(3)拓展与运用:
若![]() ,正方形
,正方形![]() 在绕点
在绕点![]() 旋转过程中,当
旋转过程中,当![]() 三点在一条直线上时,则
三点在一条直线上时,则![]() .
.
【答案】(1)![]() 证明见解析;
证明见解析;![]() ;(2)线段
;(2)线段![]() 与
与![]() 之间的数量关系为
之间的数量关系为![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)①由![]() 、
、![]() 结合
结合![]() 可得四边形CEGF是矩形,再由
可得四边形CEGF是矩形,再由![]() 即可得证;
即可得证;
②由正方形性质知![]() 、
、![]() ,据此可得
,据此可得![]() 、
、![]() ,利用平行线分线段成比例定理可得;
,利用平行线分线段成比例定理可得;
(2)连接CG,只需证![]() 即可得;
即可得;
(3)由(2)证出![]() 就可得到
就可得到![]() ,再根据
,再根据![]() 三点在同一直线上分在CD左边和右边两种不同的情况求出AG的长度,即可求出BE的长度.
三点在同一直线上分在CD左边和右边两种不同的情况求出AG的长度,即可求出BE的长度.
(1)![]() 证明:
证明:![]() 四边形
四边形![]() 是正方形,
是正方形,
![]()
![]()
![]()
![]() 四边形
四边形![]() 是矩形,
是矩形,![]()
![]()
![]() 四边形
四边形![]() 是正方形;
是正方形;
![]() 解:由①知四边形CEGF是正方形,
解:由①知四边形CEGF是正方形,
∴∠CEG=∠B=90°,∠ECG=45°,
∴![]() ,GE∥AB,
,GE∥AB,
∴![]()
故答案为:![]() .
.
(2)如下图所示连接![]() 由旋转性质知
由旋转性质知![]()
在![]() 和
和![]() 中,
中,![]()
![]()
![]() ,
,
![]()
![]()
![]() 线段
线段![]() 与
与![]() 之间的数量关系为
之间的数量关系为![]() ;
;
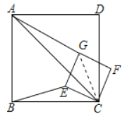
(3)解:![]() 当正方形
当正方形![]() 在绕点
在绕点![]() 旋转到如下图所示时:
旋转到如下图所示时:
当![]() 三点在一条直线上时,
三点在一条直线上时,
由(2)可知![]() ,
,
![]() ,
,
![]()
![]() ∠CEG=∠CEA=∠ABC=90°,
∠CEG=∠CEA=∠ABC=90°,![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
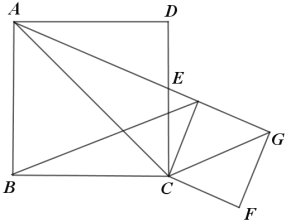
![]() 当正方形
当正方形![]() 在绕点
在绕点![]() 旋转到如下图所示时:
旋转到如下图所示时:
当![]() 三点在一条直线上时,
三点在一条直线上时,
由(2)可知![]() ,
,
![]() ,
,
![]()
![]() ∠CEA=∠ABC=90°,
∠CEA=∠ABC=90°,![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
故答案为:![]() 或
或![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】![]() 年,我省中考体育分值增加到
年,我省中考体育分值增加到![]() 分,其中女生必考项目为八百米跑,我校现抽取九年级部分女生进行八百米测试成绩如下:
分,其中女生必考项目为八百米跑,我校现抽取九年级部分女生进行八百米测试成绩如下:
成绩 |
|
|
|
|
|
等级 |
|
|
|
|
|
百分比 |
|
|
|
|
|
(1)求样本容量及表格中的![]() 和
和![]() 的值
的值
(2)求扇形统计图中![]() 等级所对的圆心角度数,并补全统计图.
等级所对的圆心角度数,并补全统计图.
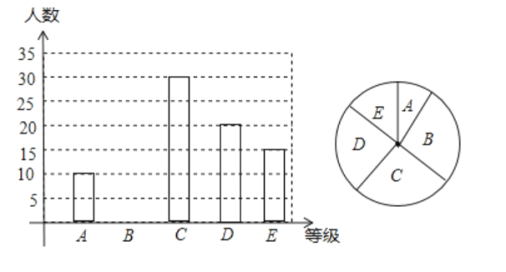
(3)我校![]() 年级共有女生
年级共有女生![]() 人.若女生八百米成绩的达标成绩为
人.若女生八百米成绩的达标成绩为![]() 分,我校九年级女生八百米成绩达标的人数有多少?
分,我校九年级女生八百米成绩达标的人数有多少?