Question

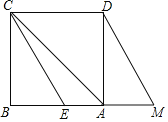
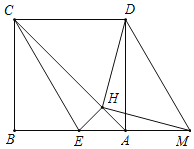
【题目】如图，已知正方形ABCD，点M是边BA延长线上的动点(不与点A重合)，且AM＜AB，△CBE由△DAM平移得到．若过点E作EH⊥AC，H为垂足，则有以下结论：

①点M位置变化，使得∠DHC＝60°时，2BE＝DM；

②无论点M运动到何处，都有DM＝HM；

③无论点M运动到何处，∠CHM一定大于135°．其中正确结论的序号为(　　)

A.①③B.①②C.②③D.①②③

Answer 1

【答案】D

【解析】

根据正方形的性质可证得△MEH≌△DAH，再得到△DHM是等腰直角三角形，故DM＝HM，②正确；当∠DHC＝60°时，可求得∠ADM＝45°﹣15°＝30°，故Rt△ADM中，DM＝2AM，DM＝2BE，①正确；再根据点M是边BA延长线上的动点(不与点A重合)，且AM＜AB，∠AHM＜∠BAC＝45°，即可判断.

由题可得，AM＝BE，

∴AB＝EM＝AD，

∵四边形ABCD是正方形，EH⊥AC，

∴EM＝AD，∠AHE＝90°，∠MEH＝∠DAH＝45°＝∠EAH，

∴EH＝AH，

∴△MEH≌△DAH(SAS)，

∴∠MHE＝∠DHA，MH＝DH，

∴∠MHD＝∠AHE＝90°，△DHM是等腰直角三角形，

∴DM＝HM，故②正确；

当∠DHC＝60°时，∠ADH＝60°﹣45°＝15°，

∴∠ADM＝45°﹣15°＝30°，

∴Rt△ADM中，DM＝2AM，

即DM＝2BE，故①正确；

∵点M是边BA延长线上的动点(不与点A重合)，且AM＜AB，

∴∠AHM＜∠BAC＝45°，

∴∠CHM＞135°，故③正确；

由上可得正确结论的序号为①②③．

故选：D．