题目内容
【题目】取一副三角板按如图所示拼接,固定三角板ADC,将三角板ABC绕点A顺时针方向旋转,旋转角度为α(0°<α≤45°),得到△ABC′.
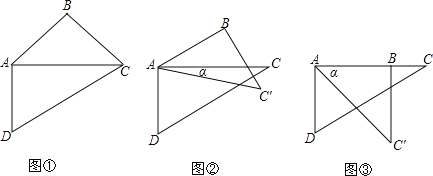
①当α为多少度时,AB∥DC?
②当旋转到图③所示位置时,α为多少度?
③连接BD,当0°<α≤45°时,探求∠DBC′+∠CAC′+∠BDC值的大小变化情况,并给出你的证明.
【答案】(1)当α=15°时,AB∥DC;(2)α=45°;(3)详见解析.
【解析】
(1)若AB∥DC,则∠BAC=∠C=30°,得到α=∠BAC′-∠BAC=45°-30°=15°;
(2)当旋转到图③所示位置时,α=45°,
(3)连接CC′,BD,BO,在△BDO和△OCC′中,利用三角形内角和定理得到∠BDO+∠DBO=∠OCC′+∠OC′C,即可求得∠DBC′+∠CAC′+∠BDC=105°,即得到∠DBC′+∠CAC′+∠BDC值的大小不变.
解:(1)当α=15°时,AB∥DC.
(2)当旋转到图③所示位置时,α=45°.
(3)当0°<α≤45°时,∠DBC′+∠CAC′+∠BDC值的大小不变.
证明:连接CC′,在△BDO和△OCC′中,对顶角∠BOD=∠COC′,
∴∠1+∠2=∠3+∠4,.
∴∠DBC′+∠CAC′+∠BDC
=∠2+∠α+∠1
=180°―∠ACD―∠AC′B
=180°―45°―30°
=105°
∴当0°<α≤45°时,∠DBC′+∠CAC′+∠BDC值的大小不变

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目