题目内容
已知在△ABC中,AB=AC,⊙O为△ABC的外接圆,CD为⊙O的直径,DM∥AC交AB于M.
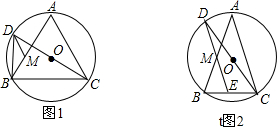
(1)如图1,若∠BAC=60゜,求证:BD=
DM;
(2)如图2,延长DM交BC于E,CE=4,CD=10,求AM的长.

(1)如图1,若∠BAC=60゜,求证:BD=
| 3 |
(2)如图2,延长DM交BC于E,CE=4,CD=10,求AM的长.
分析:(1)由题意易证△ABC是等边三角形,则CD是角平分线.根据平行线的性质和圆周角定理得到∠1=∠2=30°.然后通过解直角△DNM可以证得结论;
(2)如图2,延长DE交⊙O于点F,连接CF,AD.易证点A、O、F共线,四边形ACFD是矩形.设AF交交BC于点N,则根据垂径定理得到AN⊥BC,BN=NC.易证△CFE∽△ACF,则CF:AC=CE:AF=4:10=2:5,又CF2+AC2=AF2=100,CF2=AF•FN由此可以求得BC的长度;最后根据平行线分线段成比例可以求得线段AM的长度.
(2)如图2,延长DE交⊙O于点F,连接CF,AD.易证点A、O、F共线,四边形ACFD是矩形.设AF交交BC于点N,则根据垂径定理得到AN⊥BC,BN=NC.易证△CFE∽△ACF,则CF:AC=CE:AF=4:10=2:5,又CF2+AC2=AF2=100,CF2=AF•FN由此可以求得BC的长度;最后根据平行线分线段成比例可以求得线段AM的长度.
解答: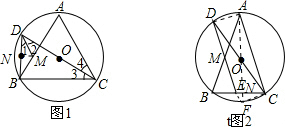 证明:(1)如图1,过点M作MN⊥BD于点N.
证明:(1)如图1,过点M作MN⊥BD于点N.
∵CD是直径,
∴∠DBC=90°.
∵在△ABC中,AB=AC,∠BAC=60゜,
∴△ABC是等边三角形,
∴∠ACB=∠ABC=60°,且CD平分∠ACB,
∴∠DBA=∠3=∠4=30°.
∴DM=BM,
∴DN=BN.
∵DM∥AC,
∴∠2=∠4=30°.
又∵∠BDC=∠A=60°,
∴∠1=∠2=30°,
∴在直角△DNM中,DM=
BD,
∴BD=
DM;
(2)如图2,延长DE交⊙O于点F,连接CF,AD.
∵DM∥AC,即DF∥AC,
∴∠DFC+∠ACF=180°.
又∵CD是直径,
∴∠DFC=90°,
∴∠ACF=90°,
∴AF是直径,
∴点A、O、F共线.易证四边形ACFD是矩形.
设AF交交BC于点N,则AN⊥BC,BN=NC,
易证△CFE∽△ACF,则CF:AC=CE:AF=4:10=2:5,
又CF2+AC2=AF2=100,
解得AC=
,CF=
,又CF2=CN•CE
∴CN=
,EN=CE-CN=
,
∴BC=2CN=
,
又∵AM:AB=CE:CB,
∴AM=
.
 证明:(1)如图1,过点M作MN⊥BD于点N.
证明:(1)如图1,过点M作MN⊥BD于点N.∵CD是直径,
∴∠DBC=90°.
∵在△ABC中,AB=AC,∠BAC=60゜,
∴△ABC是等边三角形,
∴∠ACB=∠ABC=60°,且CD平分∠ACB,
∴∠DBA=∠3=∠4=30°.
∴DM=BM,
∴DN=BN.
∵DM∥AC,
∴∠2=∠4=30°.
又∵∠BDC=∠A=60°,
∴∠1=∠2=30°,
∴在直角△DNM中,DM=
| ||
| 2 |
∴BD=
| 3 |
(2)如图2,延长DE交⊙O于点F,连接CF,AD.
∵DM∥AC,即DF∥AC,
∴∠DFC+∠ACF=180°.
又∵CD是直径,
∴∠DFC=90°,
∴∠ACF=90°,
∴AF是直径,
∴点A、O、F共线.易证四边形ACFD是矩形.
设AF交交BC于点N,则AN⊥BC,BN=NC,
易证△CFE∽△ACF,则CF:AC=CE:AF=4:10=2:5,
又CF2+AC2=AF2=100,
解得AC=
50
| ||
| 29 |
20
| ||
| 29 |
∴CN=
| 100 |
| 29 |
| 16 |
| 29 |
∴BC=2CN=
| 200 |
| 29 |
又∵AM:AB=CE:CB,
∴AM=
| 29 |
点评:本题考查了圆周角定理,矩形的判定与性质,勾股定理以及等边三角形的判定与性质.此题难度较大.

练习册系列答案
相关题目
 22、如图,已知在△ABC中,∠A=(2x+10)°,∠B=(3x)°,∠ACD是△ABC的一个外角,且∠ACD=(6x-10)°,求∠A的度数.
22、如图,已知在△ABC中,∠A=(2x+10)°,∠B=(3x)°,∠ACD是△ABC的一个外角,且∠ACD=(6x-10)°,求∠A的度数.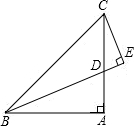 如图,已知在△ABC中,∠BAC为直角,AB=AC,D为AC上一点,CE⊥BD于E.若BD平分∠ABC.
如图,已知在△ABC中,∠BAC为直角,AB=AC,D为AC上一点,CE⊥BD于E.若BD平分∠ABC. 如图,已知在△ABC中,∠B与∠C的平分线交于点P.
如图,已知在△ABC中,∠B与∠C的平分线交于点P.