题目内容
【题目】已知：二次函数
的图象与x轴交于点A、
，顶点为
求该二次函数的解析式；
如图，过A、C两点作直线，并将线段AC沿该直线向上平移，记点A、C分别平移到点D、E处
若点F在这个二次函数的图象上，且
是以EF为斜边的等腰直角三角形，求点F的坐标；
试确定实数p，q的值，使得当
时，
．
【答案】（1）该二次函数的解析式为
；（2）点F的坐标为
；（3）满足条件的实数p，q的值为
，
或
，．
【解析】分析：（1）由二次函数y=ax2+bx+c的顶点为C（-1，-2），可设其解析式为y=a（x+1）2-2，再把B（-3，0）代入，利用待定系数法即可求出该二次函数的解析式；
（2）由二次函数的解析式求出A（1，0）．过点C作CH⊥x轴于点H．解直角△ACH，得出AH=2=CH，那么∠1=45°，AC=2
．解等腰直角△DEF得出∠2=45°，EF=4，由∠1=∠2=45°，得到EF∥CH∥y轴．利用待定系数法求出直线AC的解析式为y=x-1．设F（m，
m2+m-
）（其中m＞1），则点E（m，m-1），那么EF=（m2+m-）-（m-1）=m2-=4，解方程求出m，进而得出点F的坐标；
（3）先求出y=
时x1=-4，x2=2．再根据二次函数的性质可知，当p≤x≤q时，p≤y≤，应分三种情况讨论：①p≤x≤-1；②p＜-1≤q；③-1≤p＜q．
详解：
二次函数
的顶点为
，
可设该二次函数的解析式为
，
把
代入，得
，
解得
该二次函数的解析式为；
由
，得
或1，
．
如图，过点C作
轴于点H．
，
，
，
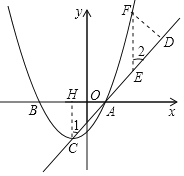
又
，
，
，
．
在等腰直角
中，
，
，
，
，
，
轴．
由
，可得直线AC的解析式为
．
由题意，设
其中
，则点
，
，
，
不合题意舍去
，
点F的坐标为；
当
时，
，解得
，
．
，
当
时，y随x的增大而减小；当
时，y随x的增大而增大；
当
时，y有最小值
．
当
时，
，
可分三种情况讨论：
当
时，由增减性得：
当
时，
，当
时，
，不合题意，舍去；
当
时，
Ⅰ若
，由增减性得：
当时，，当时，
，不合题意，舍去；
Ⅱ若
，由增减性得：
当
时，，当时，
，符合题意，
，；
当
时，由增减性得：
当时，，当
时，
，
把，
代入，得
，
解得
，
不合题意，舍去，
，．
综上所述，满足条件的实数p，q的值为，或，．
