题目内容
【题目】小莹和小亮在笔直的公路上同起点、同终点、同方向匀速步行![]() 米,先到终点的人原地休息.已知小莹先出发
米,先到终点的人原地休息.已知小莹先出发![]() 分钟,在整个步行过程中,两人的距离
分钟,在整个步行过程中,两人的距离![]() (米)与小莹出发的时间
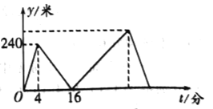
(米)与小莹出发的时间![]() (分)之间的关系如图所示,下列结论:①小莹的步行速度为
(分)之间的关系如图所示,下列结论:①小莹的步行速度为![]() 米/分;②小亮用
米/分;②小亮用![]() 分钟追上小莹;③小亮走完全程用了
分钟追上小莹;③小亮走完全程用了![]() 分钟;④小亮到达终点时,小莹离终点还有
分钟;④小亮到达终点时,小莹离终点还有![]() 米。其中正确的结论有( )
米。其中正确的结论有( )
A. ![]() 个B.
个B. ![]() 个C.
个C. ![]() 个D.
个D. ![]() 个
个
【答案】B
【解析】
先根据题意求出他们的速度,再求出他们走完全程的时间,便可求出其他问题.
小莹的速度为:240÷4=60(米/分);
小亮追上小莹所用时间:16-4=12(分);
小亮的速度为:60×16÷12=80(米/分);
小亮走完全程用时:2400÷80=30(分);
小莹走完全程用时:2400÷60=40(分);
小亮到达终点时,小莹离终点还有:2400-60×(30+4)=360(米);
∴正确的有①③.
故选:B.

【题目】为了解宣城市市民“绿色出行”方式的情况,我校数学兴趣小组以问卷调查的形式,随机调查了宣城市部分出行市民的主要出行方式(参与问卷调查的市民都只从以下五个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
种类 |
|
|
|
|
|
出行方式 | 共享单车 | 步行 | 公交车 | 的士 | 私家车 |
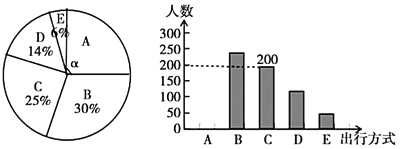
根据以上信息,回答下列问题:
(1)参与本次问卷调查的市民共有______人,其中选择![]() 类的人数有______人;
类的人数有______人;
(2)在扇形统计图中,求![]() 类对应扇形圆心角
类对应扇形圆心角![]() 的度数,并补全条形统计图;
的度数,并补全条形统计图;
(3)宣城市约有人口280万人,若将![]() 、
、![]() 、
、![]() 这三类出行方式均视为“绿色出行”方式,请估计我市“绿色出行”方式的人数.
这三类出行方式均视为“绿色出行”方式,请估计我市“绿色出行”方式的人数.
【题目】某公交公司决定更换节能环保的新型公交车![]() 购买的数量和所需费用如下表所示:
购买的数量和所需费用如下表所示:
A型数量 | B型数量 | 所需费用 |
3 | 1 | 450 |
2 | 3 | 650 |
![]() 求A型和B型公交车的单价;
求A型和B型公交车的单价;
![]() 该公司计划购买A型和B型两种公交车共10辆,已知每辆A型公交车年均载客量为60万人次,每辆B型公交车年均载客量为100万人次,若要确保这10辆公交车年均载客量总和不少于670万人次,则A型公交车最多可以购买多少辆?
该公司计划购买A型和B型两种公交车共10辆,已知每辆A型公交车年均载客量为60万人次,每辆B型公交车年均载客量为100万人次,若要确保这10辆公交车年均载客量总和不少于670万人次,则A型公交车最多可以购买多少辆?








