题目内容
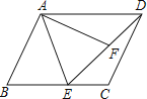
【题目】(1)如图1,![]() 为
为![]() 上一点,若
上一点,若![]() ,
,![]() ,求证:
,求证:![]() .
.

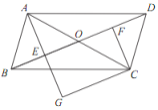
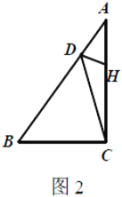
(2)如图2,![]() 中,
中,![]() ,
,![]() 为
为![]() 上一点,
上一点,![]() 为
为![]() 上一点,
上一点,![]() ,
,![]() ,
,![]() ,求
,求![]() .
.
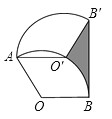
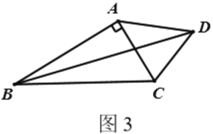
(3)如图,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,直接写出
,直接写出![]() 的长.
的长.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据相似三角形的判定,可证得![]() ,根据相似三角形的性质可得
,根据相似三角形的性质可得![]() ,再利用两边对应成比例且夹角相等这个判定就可证得
,再利用两边对应成比例且夹角相等这个判定就可证得![]() ;
;
(2)根据![]() 可以设
可以设![]() ,由
,由![]() ,
,![]() 可得
可得![]() ,根据相似的性质进而表示出BP的长,由(1)中的结论
,根据相似的性质进而表示出BP的长,由(1)中的结论![]() ,
,![]() 和CB=CD可证得
和CB=CD可证得![]() ,进而可得
,进而可得![]() ,根据相似的性质即可求出答案;
,根据相似的性质即可求出答案;
(3)过点A作AD⊥AE,与DC的延长线交于E点,根据两边成比例且夹角相等可证得![]() ,根据相似的性质可得BE的长,进而得出
,根据相似的性质可得BE的长,进而得出![]() ,由勾股定理可求出DE的长,再由30°直角三角形的性质即可求出AD的长.
,由勾股定理可求出DE的长,再由30°直角三角形的性质即可求出AD的长.
(1)证明:∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
又∵![]() ,
,
∴![]()
∴![]() .
.
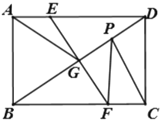
(2)作![]() 于
于![]() ,过
,过![]() 点作
点作![]() 交
交![]() 延长线于
延长线于![]() ,
,
∵![]() ,
,
∴设![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,![]()
∴∠BPC=∠ACB=90°,
∴∠B+∠BCP=90°,∠ACP+∠BCP=90°,
∴∠ACP=∠B,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]()
∴![]() ,
,![]() ,
,
由(1)得![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
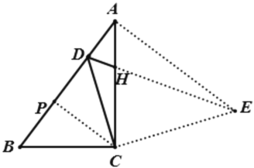
(3)过点A作AD⊥AE,与DC的延长线交于E点,如图,
∵AD⊥AE,∠BAC=90°,
∴∠BAC=∠EAD=90°,
∴∠BAE=∠CAD,
∵![]() ,
,
∴∠ABC=∠AED=30°,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,∠AEB=60°,
,∠AEB=60°,
∴![]() ,
,
在△BED中,由勾股定理得,
![]() ,
,
∴![]() .
.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目