Question

【题目】如图，在平面直角坐标系xOy中，直线y=﹣x+3与x轴交于点C，与直线AD交于点A（ ， ），点D的坐标为（0，1）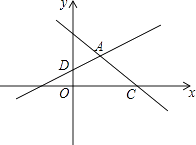
（1）求直线AD的解析式；
（2）直线AD与x轴交于点B，若点E是直线AD上一动点（不与点B重合），当△BOD与△BCE相似时，求点E的坐标．

Answer 1

【答案】
（1）解：设直线AD的解析式为y=kx+b，

将A（ ， ），D（0，1）代入得： ，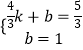

解得： ．

故直线AD的解析式为：y= x+1；

（2）∵直线AD与x轴的交点为（﹣2，0），

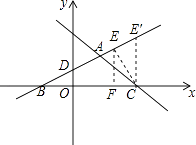
∴OB=2，

∵点D的坐标为（0，1），

∴OD=1，

∵y=﹣x+3与x轴交于点C（3，0），

∴OC=3，

∴BC=5

∵△BOD与△BEC相似，

∴ 或 ，

∴ = = 或 ，

∴BE=2 ，CE= ，或CE= ，

∵BCEF=BECE，

∴EF=2，CF= =1，

∴E（2，2），或（3， ）．

【解析】（1）设直线AD的解析式为y=kx+b，用待定系数法将A（ ， ），D（0，1）的坐标代入即可；（2）由直线AD与x轴的交点为（﹣2，0），得到OB=2，由点D的坐标为（0，1），得到OD=1，求得BC=5，根据相似三角形的性质得到 或 ，代入数据即可得到结论．
【考点精析】本题主要考查了确定一次函数的表达式和相似三角形的性质的相关知识点，需要掌握确定一个一次函数，需要确定一次函数定义式y=kx+b（k不等于0）中的常数k和b．解这类问题的一般方法是待定系数法；对应角相等，对应边成比例的两个三角形叫做相似三角形才能正确解答此题．