题目内容
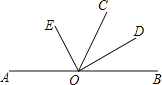
【题目】已知:A、O、B三点在同一直线上,OE、OD分别平分∠AOC、∠BOC.
(1)求∠EOD的度数;
(2)若∠AOE=50°,求∠BOC的度数.
【答案】(1)90°;(2)80°
【解析】
(1)由于OE、OD分别平分∠AOC、∠BOC,所以∠EOC=![]() ∠AOC,∠COD=
∠AOC,∠COD=![]() ∠BOC,进而得出∠EOD=∠EOC+∠COD=
∠BOC,进而得出∠EOD=∠EOC+∠COD=![]() ∠AOB=90°;
∠AOB=90°;
(2)由OE平分∠AOC,∠AOE=50°,得出∠AOC=2∠AOE=100°,再根据邻补角定义得出∠BOC=180°﹣∠AOC=80°.
(1)∵OE、OD分别平分∠AOC、∠BOC,
∴∠EOC=![]() ∠AOC,∠COD=
∠AOC,∠COD=![]() ∠BOC,
∠BOC,
∴∠EOD=∠EOC+∠COD=![]() ∠AOC+
∠AOC+![]() ∠BOC=
∠BOC=![]() ∠AOB,
∠AOB,
又∵A、O、B三点在同一直线上,
∴∠AOB=180°,
∴∠EOD=![]() ∠AOB=90°;
∠AOB=90°;
(2)∵OE平分∠AOC,∠AOE=50°,
∴∠AOC=2∠AOE=100°,
∴∠BOC=180°﹣∠AOC=80°.

练习册系列答案
 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
【题目】某校七年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下,并绘制了如图所示的两幅不完整的统计图,请结合图中相关数据回答下列问题:
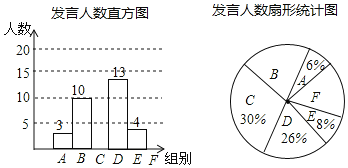
(1)直接写出随机抽取学生的人数为 人;
(2)直接补全频数直方图和扇形统计图;
(3)该校七年级共有学生1000人,请估计七年级在这天里发言次数大于等于12次的人数.
发言次数n | |
A | 0≤n<3 |
B | 3≤n<6 |
C | 6≤n<9 |
D | 9≤n<12 |
E | 12≤n<15 |
F | 15≤n<18 |