题目内容
如图,在平面直角坐标系中,双曲线 和直线y=kx+b交于A,B两点,点A的坐标为(﹣3,2),BC⊥y轴于点C,且OC=6BC.
和直线y=kx+b交于A,B两点,点A的坐标为(﹣3,2),BC⊥y轴于点C,且OC=6BC.
(1)求双曲线和直线的解析式;
(2)直接写出不等式 的解集.
的解集.
(1) ,y=﹣2x﹣4;(2)﹣3<x<0或x>1.
,y=﹣2x﹣4;(2)﹣3<x<0或x>1.
解析试题分析:(1)将A坐标代入反比例解析式中求出m的值,确定出反比例解析式,根据OC=6BC,且B在反比例图象上,设B坐标为(a,﹣6a),代入反比例解析式中求出a的值,确定出B坐标,将A与B坐标代入一次函数解析式中求出k与b的值,即可确定出一次函数解析式.
(2)根据一次函数与反比例函数的两交点A与B的横坐标,以及0,将x轴分为四个范围,找出反比例图象在一次函数图象上方时x的范围即可.
试题解析:∵点A(﹣3,2)在双曲线 上,∴
上,∴ ,解得m=﹣6.
,解得m=﹣6.
∴双曲线的解析式为 .
.
∵点B在双曲线 上,且OC=6BC,
上,且OC=6BC,
设点B的坐标为(a,﹣6a),∴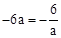 ,解得:a=±1(负值舍去).∴点B的坐标为(1,﹣6).
,解得:a=±1(负值舍去).∴点B的坐标为(1,﹣6).
∵直线y=kx+b过点A,B,
∴ ,解得:
,解得: .
.
∴直线的解析式为y=﹣2x﹣4.
(2)根据图象得:不等式 的解集为﹣3<x<0或x>1.
的解集为﹣3<x<0或x>1.
考点:1.反比例函数与一次函数的交点问题;2.曲线上点的坐标与方程的关系;3.数形结合思想的应用.

练习册系列答案
相关题目
某公司有甲种原料260kg,乙种原料270kg,计划用这两种原料生产A、B两种产品共40件.生产每件A种产品需甲种原料8kg,乙种原料5kg,可获利润900元;生产每件B种产品需甲种原料4kg,乙种原料9kg,可获利润1100元.设安排生产A种产品x件.
(1)完成下表
| | 甲(kg) | 乙(kg) | 件数(件) |
| A | | 5x | x |
| B | 4(40-x) | | 40-x |
(3)设生产这批40件产品共可获利润y元,将y表示为x的函数,并求出最大利润.

 的解;
的解; 的图象相交于点A(-2,a),并且与x轴相交于点B。
的图象相交于点A(-2,a),并且与x轴相交于点B。
 与
与 的图象相交于A点,函数
的图象相交于A点,函数 轴、
轴、 轴于点B,C,函数
轴于点B,C,函数
 的面积
的面积