Question

（本题满分12分）已知抛物线交x轴于A(1,0)、B(3,0)两点，交y轴于点C，其顶点为D．

（1）求b、c的值并写出抛物线的对称轴；

（2）连接BC，过点O作直线OE⊥BC交抛物线的对称轴于点E．

求证：四边形ODBE是等腰梯形；

（3）抛物线上是否存在点Q，使得△OBQ的面积等于四边形ODBE的面积的？若存在，求点Q的坐标；若不存在，请说明理由．

 

Answer 1

 

（1）x=2

（2）四边形ODBE是等腰梯形，证明略。

（3）存在，理由略。

解析:

（1）求出：，，抛物线的对称轴为：x=2     ……3分

(2) 抛物线的解析式为，易得C点坐标为（0，3），D点坐标为（2，-1）

设抛物线的对称轴DE交x轴于点F，易得F点坐标为（2，0），连接OD，DB，BE

∵OBC是等腰直角三角形，DFB也是等腰直角三角形，E点坐标为（2，2），

∴∠BOE= ∠OBD=   ∴OE∥BD

∴四边形ODBE是梯形                           ……5分

在和中，

OD= ，BE=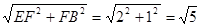

∴OD= BE

∴四边形ODBE是等腰梯形                      …7分

(3) 存在，                                            ………8分

由题意得：     ………9分

设点Q坐标为（x，y），

由题意得：=

∴

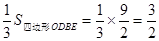
当y=1时，即，∴，，

∴Q点坐标为（2+，1）或(2-，1)               ……11分

当y=-1时，即，  ∴x=2，

∴Q点坐标为（2，-1）

综上所述，抛物线上存在三点Q（2+，1），Q (2-，1) ，Q（2，-1）

使得=．               ……12分