题目内容
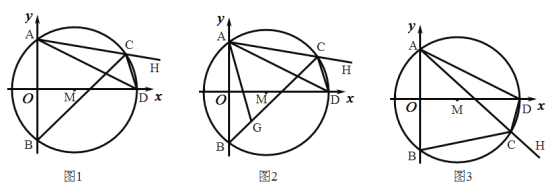
【题目】已知:抛物线y=2ax2﹣ax﹣3(a+1)与x轴交于点AB(点A在点B的左侧).
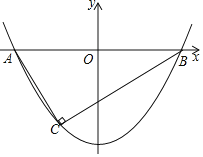
(1)不论a取何值,抛物线总经过第三象限内的一个定点C,请直接写出点C的坐标;
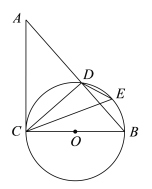
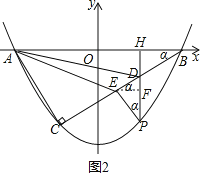
(2)如图,当AC⊥BC时,求a的值和AB的长;
(3)在(2)的条件下,若点P为抛物线在第四象限内的一个动点,点P的横坐标为h,过点P作PH⊥x轴于点H,交BC于点D,作PE∥AC交BC于点E,设△ADE的面积为S,请求出S与h的函数关系式,并求出S取得最大值时点P的坐标.
【答案】(1)第三象限内的一个定点C为(﹣1,﹣3);(2)a=![]() ,AB=
,AB=![]() ;(3)S=﹣
;(3)S=﹣![]() h2+
h2+![]() h﹣
h﹣![]() ,当h=
,当h=![]() 时,S的最大值为
时,S的最大值为![]() ,此时点P(
,此时点P(![]() ,﹣
,﹣![]() ).
).
【解析】
(1)对抛物线解析式进行变形,使a的系数为0,解出x的值,即可确定点C的坐标;
(2)设函数对称轴与x轴交点为M,根据抛物线的对称轴可求出M的坐标,然后利用勾股定理求出CM的长度,再利用直角三角形的斜边的中线等于斜边的一半求出AB的长度,则A,B两点的坐标可求,再将A,B两点代入解析式中即可求出a的值;
(3)过点E作EF⊥PH于点F,先用待定系数法求出直线BC的解析式,然后将P,D的坐标用含h的代数式表示出来,最后利用S=S△ABE﹣S△ABD=![]() ×AB×(yD﹣yE)求解
×AB×(yD﹣yE)求解
(1)y=2ax2﹣ax﹣3(a+1)=a(2x2﹣x﹣3)﹣3,
令2x2﹣x﹣3=0,解得:x=![]() 或﹣1,
或﹣1,
故第三象限内的一个定点C为(﹣1,﹣3);
(2)函数的对称轴为:x=![]() ,
,
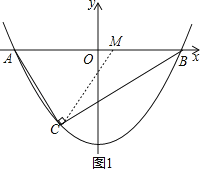
设函数对称轴与x轴交点为M,则其坐标为:(![]() ,0),
,0),
则由勾股定理得CM=![]() ,
,
则AB=2CM=![]() ,
,
∴![]()
则点A、B的坐标分别为:(﹣3,0)、(![]() ,0);
,0);
将点A的坐标代入函数表达式得:18a+3a﹣3a﹣3=0,
解得:a=![]() ,
,
函数的表达式为:y=![]() (x+3)(x﹣
(x+3)(x﹣![]() )=
)=![]() x2﹣
x2﹣![]() x﹣
x﹣![]() ;
;
(3)过点E作EF⊥PH于点F,
设:∠ABC=α,则∠ABC=∠HPE=∠DEF=α,
设直线BC的解析式为![]()
将点B、C坐标代入一次函数表达式
得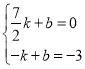 解得:
解得: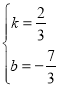
∴直线BC的表达式为:![]() ,
,
设点P(h,![]() ),则点D(h,
),则点D(h,![]() ),
),
故tan∠ABC=tanα=![]() ,则sinα=
,则sinα=![]() ,
,
yD﹣yE=DEsinα=PDsinαsinα,
S=S△ABE﹣S△ABD
=![]() ×AB×(yD﹣yE)
×AB×(yD﹣yE)
=![]()
![]()
![]()
∵﹣![]() <0,
<0,
∴S有最大值,当h=![]() 时,S的最大值为:
时,S的最大值为:![]() ,此时点P(
,此时点P(![]() ).
).